
已知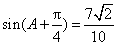 ,
,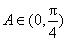 .
.
(Ⅰ)求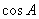 的值;
的值;
(Ⅱ)求函数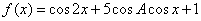 的值域.
的值域.
科目:高中数学 来源: 题型:
如图,某市准备在道路EF的一侧修建一条运动比赛道,赛道的前一部分为曲线段FBC,该曲线段是函数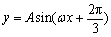
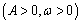 ,
,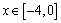 时的图象,且图象的最高点为B(-1,2)。赛道的中间部分为长
时的图象,且图象的最高点为B(-1,2)。赛道的中间部分为长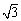 千米的直线跑道CD,且CD// EF。赛道的后一部分是以O为圆心的一段圆弧
千米的直线跑道CD,且CD// EF。赛道的后一部分是以O为圆心的一段圆弧 .
.
(1)求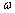 的值和
的值和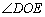 的大小;
的大小;
(2)若要在圆弧赛道所对应的扇形ODE区域内建一个“矩形草坪”,矩形的一边在道路EF上,一个顶点在半径OD上,另外一个顶点P在圆弧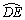 上,且
上,且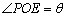 ,求当“矩形草坪”的面积取最大值时
,求当“矩形草坪”的面积取最大值时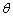 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com