已知函数f(x)=x2+3x|x-a|,其中a∈R.
(1)当a=2时,把函数f(x)写成分段函数的形式;
(2)当a=2时,求f(x)在区间[1,3]上的最值;
(3)设a≠0,函数f(x)在(m,n)上既有最大值又有最小值,请分别求出m、n的取值范围(用a表示).
解:(1)当a=2时,f(x)=x
2+3x|x-a|=
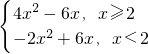
. …..4分
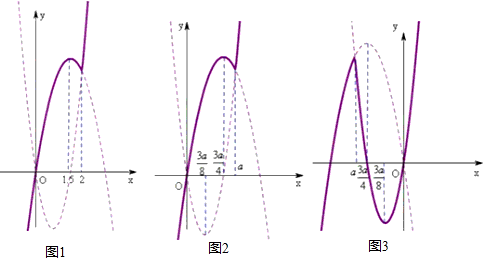
(2)结合函数f(x)的图象(图1)可得,f(1)=4,f(2)=4,f(3)=18,f(

)=

,
所以函数在区间[1,3]上最大值为18,最小值为4.…..8分
(3)当a>0时,函数的图象如图2所示,要使得在开区间(m,n)有最大值又有最小值,则最小值一定在x=a处取得,最大值在x=

a处取得;
又f(a)=a
2,在区间(-∞,a)内,函数值为a
2时,x=

,所以

≤m<
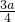
.
f(
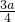
)=
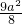
,而在区间(a,+∞)内函数值为
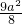
时,
x=
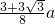
,所以,a<n≤
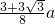
.…..12分
当a<0时,函数的图象如图3所示,要使得在开区间(m,n)有最大值又有最小值,则最大值一定在x=a处取得,最小值在x=
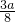
处取得,
f(a)=a
2,在(a,+∞)内函数值为 a
2 时,x=-

,所以,
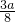
<n≤-

,f(
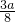
)=-

,在区间(-∞,a)内,函数值为-

时,
x=
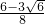
a,所以
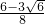
a≤m<a.…..15分
综上所述,当a>0时,

≤m<
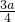
,a<n≤
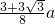
.
当a<0时,
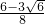
a≤m<a,
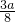
<n≤-

.…..16分.
分析:(1)当a=2时,f(x)=x
2+3x|x-a|=
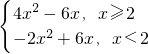
.
(2)结合函数f(x)的图象(图1)可得函数在区间[1,3]上最大值为f(3)=18,最小值为f(2)=4.
(3)当a>0时,函数的图象如图2所示,最小值一定在x=a处取得,最大值在x=

a处取得,由此求出m、n的取值范围.当a<0时,函数的图象如图3所示,最大值一定在x=a处取得,最小值在x=
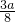
处取得,由此求出m、n的取值范围,综合可得结论.
点评:本题主要考查带有绝对值的函数,求二次函数在闭区间上的最值,体现了转化、数形结合的数学思想,属于中档题.

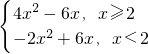 . …..4分
. …..4分 )=
)= ,
, a处取得;
a处取得; ,所以
,所以 ≤m<
≤m<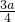 .
.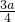 )=
)=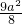 ,而在区间(a,+∞)内函数值为
,而在区间(a,+∞)内函数值为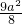 时,
时,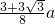 ,所以,a<n≤
,所以,a<n≤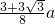 .…..12分
.…..12分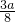 处取得,
处取得, ,所以,
,所以,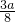 <n≤-
<n≤- ,f(
,f(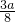 )=-
)=- ,在区间(-∞,a)内,函数值为-
,在区间(-∞,a)内,函数值为- 时,
时,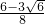 a,所以
a,所以 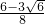 a≤m<a.…..15分
a≤m<a.…..15分 ≤m<
≤m<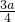 ,a<n≤
,a<n≤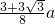 .
.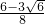 a≤m<a,
a≤m<a,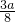 <n≤-
<n≤- .…..16分.
.…..16分.
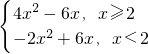 .
.  a处取得,由此求出m、n的取值范围.当a<0时,函数的图象如图3所示,最大值一定在x=a处取得,最小值在x=
a处取得,由此求出m、n的取值范围.当a<0时,函数的图象如图3所示,最大值一定在x=a处取得,最小值在x=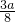 处取得,由此求出m、n的取值范围,综合可得结论.
处取得,由此求出m、n的取值范围,综合可得结论.

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<