解:(1)求导函数可得f′(x)=3x
2+2ax-2,
∵函数f(x)在(-

,1)上单调递减,在(1,+∞)上单调递增,
∴x=1是方程f′(x)=0的根,解得a=-

…..(3分)
(2)由题意得:f′(x)=3x
2+2ax-2≤0在(-2,

)上恒成立,
∴

,∴

,∴

…..(7分)
(3)当a=-

时,f(x)=x
3-

x
2-2x+5,,
由f′(x)=0得x=-

或1
列表:
| x | -1 | (-1,- ) ) | - | (- ,1) ,1) | 1 | (1,2) | 2 |
| f′(x) | | + | 0 | - | 0 | + | |
| f(x) |  | | 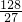 | |  | | 7 |
∴x∈(-1,2)时,f(x)的最小值为

,此时x=1
欲使不等式f(x)<m有解,只需m≥[f(x)]
min=

∴实数m的取值范围为[

,+∞). …(12分)
分析:(1)求导函数,根据函数f(x)在(-

,1)上单调递减,在(1,+∞)上单调递增,可得x=1是方程f′(x)=0的根,从而可求实数a的值;
(2)由题意得:f′(x)=3x
2+2ax-2≤0在(-2,

)上恒成立,由此可实数a的取值范围;
(3)求导函数,求导函数x∈(-1,2)时,f(x)的最小值,欲使不等式f(x)<m有解,只需m≥[f(x)]
min,从而可求实数m的取值范围.
点评:本题考查导数知识的运用,考查恒成立问题,考查函数的最值,区分恒成立与有解是解题的关键.

 ,1)上单调递减,在(1,+∞)上单调递增,求实数a的值;
,1)上单调递减,在(1,+∞)上单调递增,求实数a的值; )上单调递减,若存在,试求a的取值范围;若不存在,请说明理由;
)上单调递减,若存在,试求a的取值范围;若不存在,请说明理由; ,当x∈(-1,2)时不等式f(x)<m有解,求实数m的取值范围.
,当x∈(-1,2)时不等式f(x)<m有解,求实数m的取值范围. ,1)上单调递减,在(1,+∞)上单调递增,
,1)上单调递减,在(1,+∞)上单调递增, …..(3分)
…..(3分) )上恒成立,
)上恒成立, ,∴
,∴ ,∴
,∴ …..(7分)
…..(7分) 时,f(x)=x3-
时,f(x)=x3- x2-2x+5,,
x2-2x+5,, 或1
或1 )
)
 ,1)
,1)
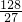

 ,此时x=1
,此时x=1
 ,+∞). …(12分)
,+∞). …(12分) ,1)上单调递减,在(1,+∞)上单调递增,可得x=1是方程f′(x)=0的根,从而可求实数a的值;
,1)上单调递减,在(1,+∞)上单调递增,可得x=1是方程f′(x)=0的根,从而可求实数a的值; )上恒成立,由此可实数a的取值范围;
)上恒成立,由此可实数a的取值范围;

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<