练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知抛物线的焦点为，过点作斜率为的直线交抛物线于两点.

    （1）若，求的面积；

    （2）过点分别作抛物线的两条切线，且直线与直线相交于点，问：点是否在某条定直线上？若在，求该定直线的方程；若不在，请说明理由.

    【答案】（1）； （2）.

    【解析】

    （1）若，则直线的方程是.联立,求得和焦点到直线的距离是，即可求得答案；

    （2）由得，设，，则，

    由，，设直线的方程为，化为，结合已知，即可求得答案.

    （1）若，则直线的方程是.

    联立消去得，不妨设点在轴上方，

    设点，，则

    则.

    而焦点到直线的距离是，

    的面积为.

    （2）由得，

    设，，则，

    由，，

    设直线的方程为，化为，

    联立方程消去

    得：，

    有，

    ，

    则直线的方程为，

    同理，直线的方程为，

    联立方程消去

    得：，

    有，

    点在定直线上.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某市为了解本市万名学生的汉字书写水平，在全市范围内进行了汉字听写考试，发现其成绩服从正态分布，现从某校随机抽取了名学生，将所得成绩整理后，绘制出如图所示的频率分布直方图.

    （1）估算该校名学生成绩的平均值（同一组中的数据用该组区间的中点值作代表）；

    （2）求这名学生成绩在内的人数；

    （3）现从该校名考生成绩在的学生中随机抽取两人，该两人成绩排名（从高到低）在全市前名的人数记为，求的分布列和数学期望.

    参考数据：若，则，

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点．

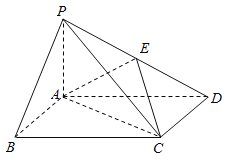
    (1) 证明：PB∥平面AEC

    (2) 设二面角D-AE-C为60°，AP=1，AD=，求三棱锥E-ACD的体积

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线的焦点为F，直线与抛物线C相切于点P，过点P作抛物线C的割线PQ，割线PQ与抛物线C的另一交点为Q，A为PQ的中点.过A作y轴的垂线与y轴交于点H，与直线l相交于点N，M为线段AN的中点.

    （1）求抛物线C的方程；

    （2）求证：点M在抛物线C上.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】共享单车又称为小黄车，近年来逐渐走进了人们的生活，也成为减少空气污染，缓解城市交通压力的一种重要手段．为调查某地区居民对共享单车的使用情况，从该地区居民中按年龄用随机抽样的方式随机抽取了人进行问卷调查，得到这人对共享单车的评价得分统计填入茎叶图，如下所示（满分分）：

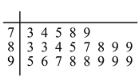
    （1）请计算这位居民问卷的平均得分；

    （2）若成绩在分以上问卷中从中任取份，求这份试卷的成绩都在以上（含分）的概率；

    （3）从成绩在分以上（含分）的居民中挑选人参加深入探讨，记抽取的个居民中成绩为分的人数为，求的分布列与期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲、乙、丙、丁四位生物学专家在筛选临床抗病毒药物，，，时做出如下预测：

    甲说：和都有效；

    乙说：和不可能同时有效；

    丙说：有效；

    丁说：和至少有一种有效.

    临床试验后证明，有且只有两种药物有效，且有且只有两位专家的预测是正确的，由此可判断有效的药物是（ ）

    A.和B.和C.和D.和

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，（其中）的图象与x轴的交点中，相邻两个交点之间的距离为，且图象上一个最低点为．

    （Ⅰ）求的解析式；

    （Ⅱ）当，求的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】私家车的尾气排放是造成雾霾天气的重要因素之一，因此在生活中我们应该提倡低碳生活，少开私家车，尽量选择绿色出行方式，为预防雾霾出一份力．为此，很多城市实施了机动车车尾号限行，我市某报社为了解市区公众对“车辆限行”的态度，随机抽查了人，将调查情况进行整理后制成下表：

    年龄（岁）

    频数

    赞成人数

    （）完成被调查人员的频率分布直方图．

    （）若从年龄在，的被调查者中各随机选取人进行追踪调查，求恰有人不赞成的概率．

    （）在在条件下，再记选中的人中不赞成“车辆限行”的人数为，求随机变量的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知Sn是正项数列{an}的前n项和，且满足a1＝4，6Sn＝an2+3an+λ（n∈N*，λ∈R），设bn＝（n﹣μ）an，若b2是数列{bn}中唯一的最小项，则实数μ的取值范围是_____.

    查看答案和解析>>

    同步练习册答案