
分析 如图所示,F($\frac{p}{2}$,0).|由于AB∥x轴,|CF|=2|AF|,|AB|=|AF|,可得|CF|=2|AB|=3p,|CE|=2|BE|.利用抛物线的定义可得xA,代入可取yA,再利用S△ACE=$\frac{2}{3}×\frac{1}{2}×\frac{3p}{2}×\sqrt{2}p$,即可得出.
解答 解:如图所示,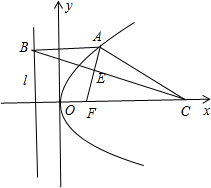 F($\frac{p}{2}$,0).|CF|=3p.
F($\frac{p}{2}$,0).|CF|=3p.
∵AB∥x轴,|CF|=2|AF|,|AB|=|AF|,
∴|CF|=2|AB|=3p,|CE|=2|BE|.
∴xA+$\frac{p}{2}$=$\frac{3p}{2}$,解得xA=p,
代入可取yA=$\sqrt{2}$p,
∴S△ACE=$\frac{2}{3}×\frac{1}{2}×\frac{3p}{2}×\sqrt{2}p$=2$\sqrt{2}$,
解得p=2.
故答案为:2.
点评 本题考查了抛物线的定义及其性质、平行线的性质、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | [0,1] | C. | [-2,2] | D. | [0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
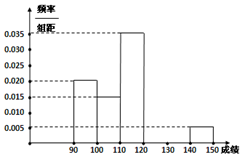 某班高三期中考试后,对考生的数学成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分成六组,第一组[90,100)、第二组[100,110)…第六组[140,150].得到频率分布直方图如图所示,若第四、五、六组的人数依次成等差数列,且第六组有2人
某班高三期中考试后,对考生的数学成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分成六组,第一组[90,100)、第二组[100,110)…第六组[140,150].得到频率分布直方图如图所示,若第四、五、六组的人数依次成等差数列,且第六组有2人查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{5}}{5}$ | B. | $\frac{3\sqrt{5}}{4}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,$\frac{1}{2}$) | C. | [$\frac{1}{4}$,1) | D. | [$\frac{1}{4}$,$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com