
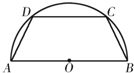
 如图,半径为2的半圆有一内接梯形ABCD,它的下底AB是⊙O的直径,上底CD的端点在圆周上.若双曲线以A,B为焦点,且过C,D两点,则当梯形ABCD的周长最大时,双曲线的实轴长为( )
如图,半径为2的半圆有一内接梯形ABCD,它的下底AB是⊙O的直径,上底CD的端点在圆周上.若双曲线以A,B为焦点,且过C,D两点,则当梯形ABCD的周长最大时,双曲线的实轴长为( )A、
| ||
B、2
| ||
C、
| ||
D、2
|
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |


 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:
| 3 |
| π |
| 3 |
| A、f1(x),f2(x),f3(x)两两为“同形”函数 |
| B、f1(x),f2(x),f3(x)两两不为“同形”函数 |
| C、f1(x),f2(x)为“同形”函数,且它们与f3(x) 不为“同形”函数 |
| D、f2(x),f3(x)为“同形”函数,且它们与f1(x) 不为“同形”函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:
A、通过最小二乘法得到的线性回归直线经过样本的中心(
| ||||
B、用最小二乘法求回归直线方程,是寻求使
| ||||
| C、在回归分析中,变量间的关系若是非确定性关系,但因变量也能由自变量唯一确定 | ||||
| D、如果回归系数是负的,y的值随x的增大而减小 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 65 |
| 81 |
A、
| ||
B、
| ||
C、
| ||
| D、以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| 4 |
| 3 |
| π |
| 4 |
| π |
| 3 |
| α | ||
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com