
分析 根据函数的单调性和奇偶性将问题转化为|x+1|>|2x-1|,解出即可.
解答 解:∵f(x)=log${\;}_{\frac{1}{e}}}$(x2+$\frac{1}{e}$)-|${\frac{x}{e}}$|,
∴f(-x)=f(x),
∴f(x)是偶函数,
x>0时,f(x)=log${\;}_{\frac{1}{e}}}$(x2+$\frac{1}{e}$)-${\frac{x}{e}}$,
∴f(x)为减函数,
∴当x<0时,f(x)为增函数
若f(x+1)<f(2x-1),
则|x+1|>|2x-1|,解得:0<x<2,
故答案为:(0,2).
点评 本题考查了函数的单调性、奇偶性问题,考查转化思想,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
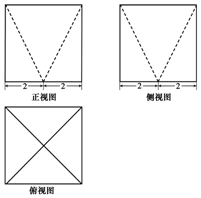 某几何体的三视图如图所示,图中的四边形都是边长为4的正方形,两条虚线互相垂直,则该几何体的表面积是( )
某几何体的三视图如图所示,图中的四边形都是边长为4的正方形,两条虚线互相垂直,则该几何体的表面积是( )| A. | $96+16\sqrt{5}$ | B. | $80+16\sqrt{5}$ | C. | $80+32\sqrt{5}$ | D. | $96+32\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
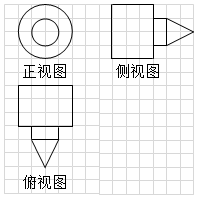 放烟花是逢年过节一种传统庆祝节日的方式.已知一种烟花模型的三视图如图中的粗实线所示,网格纸上小正方形的边长为1,则该烟花模型的表面积为(
放烟花是逢年过节一种传统庆祝节日的方式.已知一种烟花模型的三视图如图中的粗实线所示,网格纸上小正方形的边长为1,则该烟花模型的表面积为(| A. | $(18+\sqrt{3})π$ | B. | $(21+\sqrt{3})π$ | C. | $(18+\sqrt{5})π$ | D. | $(21+\sqrt{5})π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | men<nem | B. | men>nem | C. | mlnn>nlnm | D. | mlnn<nlnm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com