
【题目】选修4-4:极坐标与参数方程
在极坐标系下,已知圆O:![]() 和直线
和直线![]()
(1)求圆O和直线l的直角坐标方程;
(2)当![]() 时,求直线l与圆O公共点的一个极坐标.
时,求直线l与圆O公共点的一个极坐标.
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,点
中,点![]() 在倾斜角为
在倾斜角为![]() 的直线
的直线![]() 上,以坐标原点
上,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的方程为
的方程为![]() .
.
(1)写出![]() 的参数方程及
的参数方程及![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们把平面内与直线垂直的非零向量称为直线的法向量,在平面直角坐标系中,利用求动点轨迹方程的方法,可以求出过点![]() ,且法向量为
,且法向量为![]() 的直线(点法式)方程为:
的直线(点法式)方程为:![]() ,化简得
,化简得![]() .类比以上方法,在空间直角坐标系中,经过点
.类比以上方法,在空间直角坐标系中,经过点![]() ,且法向量为
,且法向量为![]() 的平面的方程为( )
的平面的方程为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ,
,![]() .
.
(1)当a=2时,求函数g(x)的零点;
(2)若函数g(x)有四个零点,求a的取值范围;
(3)在(2)的条件下,记g(x)的四个零点分别为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)数列{an}的前n项和为Sn=10n﹣n2,求数列{|an|}的前n项和.
(2)已知等差数列{an}满足a2=0,a6+a8=﹣10.求数列{![]() }的前n项和.
}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数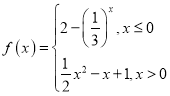 .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)画出该函数的图象,并写出该函数的单调区间(不用证明);
(3)若函数![]() 恰有3个不同零点,求实数
恰有3个不同零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为创建国家级文明城市,某城市号召出租车司机在高考期间至少参加一次“爱心送考”,该城市某出租车公司共200名司机,他们参加“爱心送考”的次数统计如图所示.
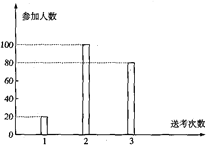
(1)求该出租车公司的司机参加“爱心送考”的人均次数;
(2)从这200名司机中任选两人,设这两人参加送考次数之差的绝对值为随机变量![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场销售价与上市时间的关系用图(1)的一条折线表示;西红柿的种植成本与上市时间的关系用图(2)的抛物线段表示.


(1)写出图(1)表示的市场售价与时间的函数关系式![]() 写出图(2)表示的种植成本与时间的函数关系式
写出图(2)表示的种植成本与时间的函数关系式![]()
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿收益最大?(注:市场售价和种植成本的单位:元/![]() kg,时间单位:天.)
kg,时间单位:天.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,若双曲线上存在点
,若双曲线上存在点![]() ,使
,使![]() ,则该双曲线的离心率
,则该双曲线的离心率![]() 范围为( )
范围为( )
A. (1,1![]() ) B. (1,1
) B. (1,1![]() ) C. (1,1
) C. (1,1![]() ] D. (1,1
] D. (1,1![]() ]
]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com