Question

在△ABC中，已知AB=

4 6

3

，cosB=

6

6

，AC边上的中线BD=

5

，求sinA的值．

Answer 1

分析：解三角形的特征是把题目中所给的条件全部集合到一个三角形中，依次解出边、角，达到解三角形的目的．
方法一通过充分利用D是中点，构造新三角形，在新三角形中解出BC的一半求出BC，再由余弦定理求边AC，下则可用正弦定理求出sinA；
方法二根据所给的条件巧妙地建立了一个直角坐标系，将三角问题转化到向量中研究，大大降低了分析问题的难度，首先是求出了

AB

，

AC

两个向量，利用公式求出了两个向量的夹角A的余弦，再求正弦．此法越过了构造新三角形，使得方法易想．
方法三与方法一类似构造了一系列的新三角形，此方法充分利用D是中点这一性质构造出了一个平行四边形，使得求三角形的另两边的边长时视野开阔，方法也较巧妙．

解答：解：解法一：设E为BC的中点，连接DE，则DE∥AB，且DE=

1

2

AB=

2 6

3

，设BE=x．
由DE∥AB可得出∠BED=π-∠B，即cos∠BED=-

6

6

在△BDE中利用余弦定理可得：BD²=BE²+ED²-2BE•EDcos∠BED，5=x²+

8

3

+2×

2 6

3

×

6

6

x，
解得x=1，x=-

7

3

（舍去）．
故BC=2，从而AC²=AB²+BC²-2AB•BCcosB=

28

3

，即AC=

2 21

3

又sinB=

30

6

，故

2

sinA

=

2 21 3

30 6

，sinA=

70

14

．

解法二：以B为坐标原点，

BC

为x轴正向建立直角坐标系，且不妨设点A位于第一象限．
由sinB=

30

6

，则

BA

=（

4 6

3

cosB，

4 6

3

sinB）=（

4

3

，

4 5

3

），
设

BC

=（x，0），则

BD

=（

4+3x

6

，

2 5

3

）．
由条件得|

.

BD

|=

( 4+3x 6 )2+( 2 5 3 )2

=

5

．
从而x=2，x=-

14

3

（舍去）．故

CA

=（-

2

3

，

4 5

3

）．
于是cosA=

BA • CA

| BA |•| CA |

=

- 8 9 + 80 9

16 9 + 80 9 • 4 9 + 80 9

=

3 14

14

．
∴sinA=

1-cos2A

=

70

14

．

解法三：过A作AH⊥BC交BC于H，延长BD到P使BD=DP，连接AP、PC．
过P做PN⊥BC交BC的延长线于N，则HB=ABcosB=

4

3

，AH=

4 5

3

，
BN=

BP2-PN2

=

BP2-AH2

=

(2 5 )2-( 4 5 3 )2

=

10

3

，
而 HB=

4

3

，∴CN=

4

3

，HC=

2

3

，AC=

AH2+HC2

=

2 21

3

．
故由正弦定理得

2

sinA

=

2 21 3

30 6

，∴sinA=

70

14

．

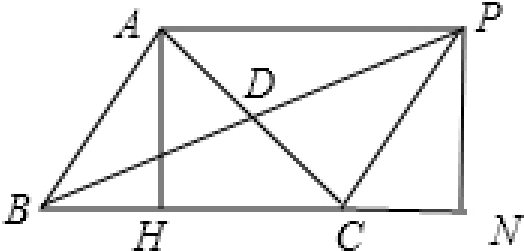
点评：构造法解三角形，如果条件不在一个三角形中时首先要做的就是把这些条件转化到一个新构造出来的三角形中，此三角形与要研究的三角形之间必有确定的关系，通过解新三角形来达到解要研究三角形的目的．
利用三角与向量之间的关系转化到向量中去也是解三角形的一个好办法，此法大大降低了解三角形时思维的深度，方法较好，数学解题中的一个重要能力就是灵活转化，本题能起到培养答题者转化化归意识的一道好题．