
【题目】已知函数f(x)=2cosx(sinx+cosx). (Ⅰ)求f( ![]() )的值;
)的值;
(Ⅱ)求函数f(x)的最小正周期及单调递增区间.
【答案】解:(Ⅰ)∵函数f(x)=2cosx(sinx+cosx)=sin2x+1+cos2x= ![]() sin(2x+
sin(2x+ ![]() )+1, ∴f(
)+1, ∴f( ![]() )=
)= ![]() sin(
sin( ![]() +
+ ![]() )+1=
)+1= ![]() sin
sin ![]() +1=
+1= ![]() +1=2.
+1=2.
(Ⅱ)∵函数f(x)= ![]() sin(2x+
sin(2x+ ![]() )+1,故它的最小正周期为
)+1,故它的最小正周期为 ![]() =π.
=π.
令2kπ﹣ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,求得kπ﹣
,k∈Z,求得kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,
,
故函数的单调递增区间为[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈Z
],k∈Z
【解析】(Ⅰ)利用三角恒等变换化简函数的解析式为f(x)= ![]() sin(2x+
sin(2x+ ![]() )+1,从而求得f(
)+1,从而求得f( ![]() )的值.(Ⅱ)根据函数f(x)=
)的值.(Ⅱ)根据函数f(x)= ![]() sin(2x+
sin(2x+ ![]() )+1,求得它的最小正周期.令2kπ﹣
)+1,求得它的最小正周期.令2kπ﹣ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,求得x的范围,可得函数的单调递增区间.
,k∈Z,求得x的范围,可得函数的单调递增区间.
【考点精析】解答此题的关键在于理解二倍角的正弦公式的相关知识,掌握二倍角的正弦公式:![]() ,以及对二倍角的余弦公式的理解,了解二倍角的余弦公式:
,以及对二倍角的余弦公式的理解,了解二倍角的余弦公式:![]() .
.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() ,
, ![]() (
(![]() ).
).
(1)求函数![]() 的单调增区间;
的单调增区间;
(2)当![]() 时,记
时,记![]() ,是否存在整数
,是否存在整数![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 有解?若存在,请求出
有解?若存在,请求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
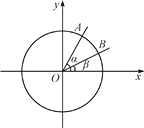
【题目】如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为![]() ,
, ![]() .求:
.求:
(1)tan(α+β)的值;
(2)α+2β的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
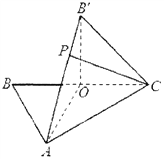
【题目】如图, ![]() 中,
中, ![]() 是
是![]() 的中点,
的中点, ![]() ,将
,将![]() 沿
沿![]() 折起,使
折起,使![]() 点到达
点到达![]() 点.
点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 的体积最大时,试问在线段
的体积最大时,试问在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ?若存在,求出点
?若存在,求出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】利用独立性检验的方法调查大学生的性别与爱好某项运动是否有关,通过随机询问110名不同的大学生是否爱好某项运动,利用![]() 列联表,由计算可得
列联表,由计算可得![]()
P(K2>k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参照附表,得到的正确结论是( )
A.有99.5%以上的把握认为“爱好该项运动与性别无关”
B.有99.5%以上的把握认为“爱好该项运动与性别有关”
C.在犯错误的概率不超过0.05%的前提下,认为“爱好该项运动与性别有关”
D.在犯错误的概率不超过0.05%的前提下,认为“爱好该项运动与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题中:
①某地市高三理科学生有15000名,在一次调研测试中,数学成绩![]() 服从正态分布
服从正态分布![]() ,已知
,已知![]() ,若按成绩分层抽样的方式抽取100份试卷进行分析,则应从120分以上(包括120分)的试卷中抽取
,若按成绩分层抽样的方式抽取100份试卷进行分析,则应从120分以上(包括120分)的试卷中抽取![]() 份;
份;
②已知命题![]() ,则
,则![]() :
:![]() ;
;
③在![]() 上随机取一个数
上随机取一个数![]() ,能使函数
,能使函数![]() 在
在![]() 上有零点的概率为
上有零点的概率为![]() ;
;
④设![]() ,则“
,则“![]() ”是“
”是“![]() ”的充要条件.
”的充要条件.
其中真命题的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,则时速在[50,70)的汽车大约( ) 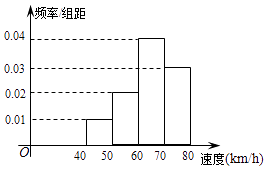
A.60辆
B.80辆
C.100辆
D.120辆
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com