
| A. | [-1,10] | B. | (-∞,-1)∪[10,+∞] | C. | R | D. | (-∞,-1]∪[10,+∞) |
分析 由指数函数的单调性化指数不等式为一元二次不等式求解.
解答 解:由($\frac{1}{2}$)${\;}^{2{x}^{2}-6x+9}$≤($\frac{1}{2}$)${\;}^{{x}^{2}+3x+19}$,得2x2-6x+9≥x2+3x+19,
即x2-9x-10≥0,解得x≤-1或x≥10.
∴不等式($\frac{1}{2}$)${\;}^{2{x}^{2}-6x+9}$≤($\frac{1}{2}$)${\;}^{{x}^{2}+3x+19}$的解集是(-∞,-1]∪[10,+∞).
故选:D.
点评 本题考查指数不等式的解法,考查数学转化思想方法,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{75}{2}$ | B. | $\frac{{75\sqrt{3}}}{2}$ | C. | $\frac{{75\sqrt{2}}}{2}$ | D. | $\frac{{75\sqrt{6}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
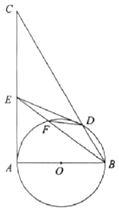 如图,在△ABC中,∠BAC=90°,以AB为直径的⊙O交BC于点D,E是边AC上一点,BE与⊙O交于点F,连接DF.
如图,在△ABC中,∠BAC=90°,以AB为直径的⊙O交BC于点D,E是边AC上一点,BE与⊙O交于点F,连接DF.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若l∥α,α∩β=m,则l∥m | B. | 若l⊥α,m⊥α,则l∥m | ||
| C. | 若l∥α,m∥α,则l∥m | D. | 若l∥α,m⊥l,则m⊥α |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com