
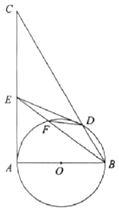
 如图,在△ABC中,∠BAC=90°,以AB为直径的⊙O交BC于点D,E是边AC上一点,BE与⊙O交于点F,连接DF.
如图,在△ABC中,∠BAC=90°,以AB为直径的⊙O交BC于点D,E是边AC上一点,BE与⊙O交于点F,连接DF.分析 (1)连接AD,证明∠C=∠DAB,∠C=∠DFB,利用∠DFE+∠DFB=180°,可得∠DFE+∠C=180°,即可证明C,D,F,E四点共圆;
(2)连接AF,根据C,D,E,F四点共圆,利用割线定理,即可求BD•BC的值.
解答 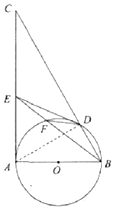 (1)证明:连接AD,
(1)证明:连接AD,
∵AB是⊙O的直径,∴∠ADB=90°,∴∠DAB+∠DBA=90°,
∵∠BAC=90°,∴∠C+∠DBA=90°,∴∠C=∠DAB,
∵$\widehat{BD}=\widehat{BD}$,∴∠DAB=∠DFB,∴∠C=∠DFB,
∵∠DFE+∠DFB=180°,∴∠DFE+∠C=180°,
∴C,D,F,E四点共圆.
(2)解:连接AF.
∵AB是⊙O的直径,∴AF⊥BE,
∵∠BAC=90°,∴AE2=EF•EB,∴52=3EB,
即$EB=\frac{25}{3}$,∴$BF=\frac{25}{3}-3=\frac{16}{3}$,
∵C,D,E,F四点共圆,∴$BD•BC=BF•BE=\frac{16}{3}×\frac{25}{3}=\frac{400}{9}$.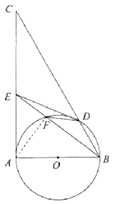
点评 本题考查四点共圆的证明,考查切割线定理的运用,考查学生分析解决问题的能力,属于中档题.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=lnx | B. | y=x3-x | C. | y=-$\frac{1}{x}$ | D. | y=ex-e-x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
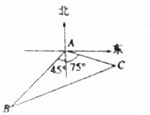 一艘客轮在航海中遇险,发出求救信号.在遇险地点A南偏西45°方向10海里的B处有一艘海难搜救艇收到求救信号后立即侦查,发现遇险客轮的航行方向为南偏东75°,正以每小时9海里的速度向一小岛靠近.已知海难搜救艇的最大速度为每小时21海里.
一艘客轮在航海中遇险,发出求救信号.在遇险地点A南偏西45°方向10海里的B处有一艘海难搜救艇收到求救信号后立即侦查,发现遇险客轮的航行方向为南偏东75°,正以每小时9海里的速度向一小岛靠近.已知海难搜救艇的最大速度为每小时21海里.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,10] | B. | (-∞,-1)∪[10,+∞] | C. | R | D. | (-∞,-1]∪[10,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com