
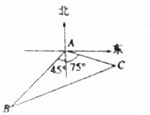
 一艘客轮在航海中遇险,发出求救信号.在遇险地点A南偏西45°方向10海里的B处有一艘海难搜救艇收到求救信号后立即侦查,发现遇险客轮的航行方向为南偏东75°,正以每小时9海里的速度向一小岛靠近.已知海难搜救艇的最大速度为每小时21海里.
一艘客轮在航海中遇险,发出求救信号.在遇险地点A南偏西45°方向10海里的B处有一艘海难搜救艇收到求救信号后立即侦查,发现遇险客轮的航行方向为南偏东75°,正以每小时9海里的速度向一小岛靠近.已知海难搜救艇的最大速度为每小时21海里.分析 (1)设搜救艇追上客轮所需时间为t小时,两船在C处相遇.由余弦定理得:BC2=AB2+AC2-2AB•AC•cos∠BAC,可得t的方程,即可得出结论;
(2)利用正弦定理,即可得出结论.
解答 解:(1)设搜救艇追上客轮所需时间为t小时,两船在C处相遇.
在△ABC中,∠BAC=45°+75°=120°,AB=10,AC=9t,BC=21t.
由余弦定理得:BC2=AB2+AC2-2AB•AC•cos∠BAC,
所以${(21t)^2}={10^2}+{(9t)^2}-2×10×9t×(-\frac{1}{2})$,
化简得36t2-9t-10=0,解得$t=\frac{2}{3}$或$t=-\frac{5}{12}$(舍去).
所以,海难搜救艇追上客轮所需时间为$\frac{2}{3}$小时.
(2)由$AC=9×\frac{2}{3}=6$,$BC=21×\frac{2}{3}=14$.
在△ABC中,由正弦定理得$sinB=\frac{AC•sin∠BAC}{BC}=\frac{{6•sin{{120}°}}}{14}=\frac{{6×\frac{{\sqrt{3}}}{2}}}{14}=\frac{{3\sqrt{3}}}{14}$.
所以角B的正弦值为$\frac{{3\sqrt{3}}}{14}$.
点评 本题考查了正弦定理与余弦定理,考查特殊角的三角函数.准确找出题中的方向角是解题的关键之处.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2) | B. | (1,+∞) | C. | [-2,1] | D. | [-1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
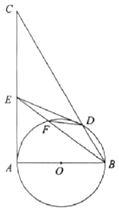 如图,在△ABC中,∠BAC=90°,以AB为直径的⊙O交BC于点D,E是边AC上一点,BE与⊙O交于点F,连接DF.
如图,在△ABC中,∠BAC=90°,以AB为直径的⊙O交BC于点D,E是边AC上一点,BE与⊙O交于点F,连接DF.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=3x+4 | B. | f(x)=4x+3 | C. | f(x)=2x+5 | D. | f(x)=5x+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com