
分析 利用同时扩大n次方倍后计算比较即可.根据题意,扩大3次方倍可得.
解答 解:∵$[(-1.8)^{\frac{2}{3}}]^{3}$=(-1.8)2=3.24,
$[{2}^{\frac{2}{3}}]^{3}$=(2)2=4
$[(-2)^{\frac{1}{3}}]^{3}$=(-2)1=-2,
所以(-1.8)${\;}^{\frac{2}{3}}}$,2${\;}^{\frac{2}{3}}}$,(-2)${\;}^{\frac{1}{3}}}$由大到小排列是:${2^{\frac{2}{3}}}>{(-1.8)^{\frac{2}{3}}}>{(-2)^{\frac{1}{3}}}$.
故答案为:${2^{\frac{2}{3}}}>{(-1.8)^{\frac{2}{3}}}>{(-2)^{\frac{1}{3}}}$.
点评 本题考查了指数幂的比较大小的方法.利用了同时扩大n次方倍.属于基础题.


 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2) | B. | (1,+∞) | C. | [-2,1] | D. | [-1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{75}{2}$ | B. | $\frac{{75\sqrt{3}}}{2}$ | C. | $\frac{{75\sqrt{2}}}{2}$ | D. | $\frac{{75\sqrt{6}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
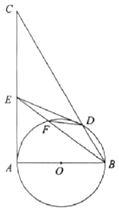 如图,在△ABC中,∠BAC=90°,以AB为直径的⊙O交BC于点D,E是边AC上一点,BE与⊙O交于点F,连接DF.
如图,在△ABC中,∠BAC=90°,以AB为直径的⊙O交BC于点D,E是边AC上一点,BE与⊙O交于点F,连接DF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com