
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 与
与![]() 轴交于
轴交于![]() 两点.以坐标原点
两点.以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求直线![]() 的普通方程及曲线
的普通方程及曲线![]() 的极坐标方程;
的极坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 在第一象限交于点
在第一象限交于点![]() ,且线段
,且线段![]() 的中点为
的中点为![]() ,点
,点![]() 在曲线
在曲线![]() 上,求
上,求![]() 的最小值.
的最小值.
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面是边长为2的正方形,侧面
的底面是边长为2的正方形,侧面![]() 底面
底面![]() ,且
,且![]() ,
,![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() 的中点.
的中点.
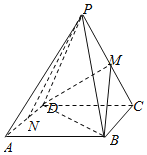
(1)求证:![]() ;
;
(2)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为提升学生的英语学习能力,进行了主题分别为“听”、“说”、“读”、“写”四场竞赛.规定:每场竞赛的前三名得分分别为![]() ,
,![]() ,
,![]() (
(![]() ,且
,且![]() ,
,![]() ,
,![]() ),选手的最终得分为各场得分之和.最终甲、乙、丙三人包揽了每场竞赛的前三名,在四场竞赛中,已知甲最终分为
),选手的最终得分为各场得分之和.最终甲、乙、丙三人包揽了每场竞赛的前三名,在四场竞赛中,已知甲最终分为![]() 分,乙最终得分为
分,乙最终得分为![]() 分,丙最终得分为
分,丙最终得分为![]() 分,且乙在“听”这场竞赛中获得了第一名,则“听”这场竞赛的第三名是( )
分,且乙在“听”这场竞赛中获得了第一名,则“听”这场竞赛的第三名是( )
A. 甲 B. 乙 C. 丙 D. 甲和丙都有可能
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 为多面体,平面
为多面体,平面![]() 与平面
与平面![]() 垂直,点
垂直,点![]() 在线段
在线段![]() 上,
上,![]()
![]() 都是正三角形.
都是正三角形.

(1)证明:直线![]() ∥面
∥面![]() ;
;
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得二面角
,使得二面角![]() 的余弦值是
的余弦值是![]() ,若不存在请说明理由,若存在请求出
,若不存在请说明理由,若存在请求出![]() 点所在的位置。
点所在的位置。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一个游戏:盒子里有![]() 个球,甲,乙两人依次轮流拿球(不放回),每人每次至少拿一个,至多拿三个,谁拿到最后一个球就算谁赢。若甲先拿,则下列说法正确的有:
个球,甲,乙两人依次轮流拿球(不放回),每人每次至少拿一个,至多拿三个,谁拿到最后一个球就算谁赢。若甲先拿,则下列说法正确的有:
__________.
①若![]() ,则甲有必赢的策略;②若
,则甲有必赢的策略;②若![]() ,则乙有必赢的策略;
,则乙有必赢的策略;
③ 若![]() ,则乙有必赢的策略;④若
,则乙有必赢的策略;④若![]() ,则甲有必赢的策略。
,则甲有必赢的策略。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】019年底,湖北省武汉市等多个地区陆续出现感染新型冠状病毒肺炎的患者,为及时有效地对疫情数据进行流行病学统计分析,某地研究机构针对该地实际情况,根据该地患者是否有武汉旅行史与是否有确诊病例接触史,将新冠肺炎患者分为四类:有武汉旅行史(无接触史),无武汉旅行史(无接触史),有武汉旅行史(有接触史)和无武汉旅行史(有接触史),统计得到以下相关数据:
(1)请将列联表填写完整,并判断能否在犯错误的概率不超过0.01的前提下,认为有武汉旅行史与有确诊病例接触史有关系?
有接触史 | 无接触史 | 总计 | |
有武汉旅行史 | 4 | ||
无武汉旅行史 | 10 | ||
总计 | 25 | 45 |
(2)已知在无武汉旅行史的10名患者中,有2名无症状感染者.现在从无武汉旅行史的10名患者中,选出2名进行病例研究,记选出无症状感染者的人数为![]() ,求
,求![]() 的分布列以及数学期望.
的分布列以及数学期望.
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将边长为2的等边△ABC沿x轴正方向滚动,某时刻A与坐标原点重合(如图),设顶点A(x,y)的轨迹方程是y=f(x),关于函数y=f(x)有下列说法:
①f(x)的值域为[0,2];
②f(x)<f(4)<f(2018);
③f(x)是周期函数且周期为6;
④滚动后,当顶点A第一次落在x轴上时,f(x)的图象与x轴所围成的图形的面积为![]() .
.
其中正确命题的序号是_____

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且与双曲线
,且与双曲线![]() 有相同的焦点.
有相同的焦点.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,点
两点,点![]() 满足
满足![]() ,点
,点![]() ,若直线
,若直线![]() 斜率为
斜率为![]() ,求
,求![]() 面积的最大值及此时直线
面积的最大值及此时直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com