
【题目】将边长为2的等边△ABC沿x轴正方向滚动,某时刻A与坐标原点重合(如图),设顶点A(x,y)的轨迹方程是y=f(x),关于函数y=f(x)有下列说法:
①f(x)的值域为[0,2];
②f(x)<f(4)<f(2018);
③f(x)是周期函数且周期为6;
④滚动后,当顶点A第一次落在x轴上时,f(x)的图象与x轴所围成的图形的面积为![]() .
.
其中正确命题的序号是_____

【答案】①③④
【解析】
先根据题意画出顶点P(x,y)的轨迹,它的轨迹是一段一段的圆弧组成的图形.从图形中可以看出,关于函数y=f(x)的说法的正确性.
根据题意画出顶点P(x,y)
的轨迹,如图所示,
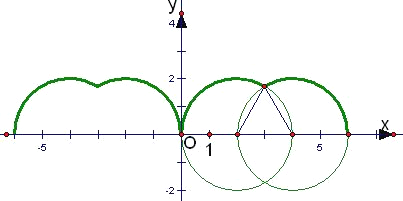
轨迹是一段一段的圆弧组成的图形,是以三角形边长为半径的圆上的圆弧,
从图形中可以看出,
关于函数y=f(x)的有下列说法:
①f(x)的值域为[0,2],①正确;
③f(x)是周期函数,周期为6,③正确;
②由于f(x)的最大值为2,(2018)=f(2)>f(4),故②不正确;
④滚动后,当顶点A第一次落在x轴上时,的图象与x轴所围成的面积为f(x)的图象在区间[0,6]上与x轴所围成的图形的面积,其大小为一个正三角形和二段扇形的面积和,
其值为![]() 故④正确,
故④正确,
故答案为:①③④.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 与
与![]() 轴交于
轴交于![]() 两点.以坐标原点
两点.以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求直线![]() 的普通方程及曲线
的普通方程及曲线![]() 的极坐标方程;
的极坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 在第一象限交于点
在第一象限交于点![]() ,且线段
,且线段![]() 的中点为
的中点为![]() ,点
,点![]() 在曲线
在曲线![]() 上,求
上,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】盒子内有3个不同的黑球,5个不同的白球.
(1)全部取出排成一列,3个黑球两两不相邻的排法有多少种?
(2)从中任取6个球,白球的个数不比黑球个数少的取法有多少种?
(3)若取一个白球记2分,取一个黑球记1分,从中任取5个球,使总分不少于7分的取法有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设关于某设备的使用年限x(年)和所支出的维修费用y万元有如下的统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)画出散点图并判断是否线性相关;
(2)如果线性相关,求线性回归方程;
(3)估计使用年限为10年时,维修费用是多少?
附注:①参考公式:回归方程![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为 ;
;
②参考数据:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,且当x≥0时,f(x)=x2﹣2x.
(1)求f(0)及f(f(1))的值;
(2)求函数f(x)的解析式;
(3)若关于x的方程f(x)﹣m=0有四个不同的实数解,求实数m的取值范围,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 市某机构为了调查该市市民对我国申办
市某机构为了调查该市市民对我国申办![]() 年足球世界杯的态度,随机选取了
年足球世界杯的态度,随机选取了![]() 位市民进行调查,调查结果统计如下:
位市民进行调查,调查结果统计如下:
支持 | 不支持 | 合计 | |
男性市民 |
| ||
女性市民 |
| ||
合计 |
|
|
(1)根据已知数据,把表格数据填写完整;
(2)利用(1)完成的表格数据回答下列问题:
(i)能否在犯错误的概率不超过![]() 的前提下认为支持申办足球世界杯与性别有关;
的前提下认为支持申办足球世界杯与性别有关;
(ii)已知在被调查的支持申办足球世界杯的男性市民中有![]() 位退休老人,其中
位退休老人,其中![]() 位是教师,现从这
位是教师,现从这![]() 位退休老人中随机抽取
位退休老人中随机抽取![]() 人,求至多有
人,求至多有![]() 位老师的概率.
位老师的概率.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com