
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
:![]() 的上顶点为
的上顶点为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,点
,点![]() ,
,![]() 在椭圆
在椭圆![]() 上,其中
上,其中![]() 是椭圆上一动点,
是椭圆上一动点,![]() 点坐标为
点坐标为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)作直线![]() 与
与![]() 轴垂直,交椭圆于
轴垂直,交椭圆于![]() ,
,![]() 两点(
两点(![]() ,
,![]() 两点均不与
两点均不与![]() 点重合),直线
点重合),直线![]() ,
,![]() 与
与![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,试求
,试求![]() 的最小值.
的最小值.
科目:高中数学 来源: 题型:
【题目】已知向量a=(-2,1),b=(x,y).
(1)若x,y分别表示将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次时第一次、第二次出现的点数,求满足a·b=-1的概率;
(2)若x,y在连续区间[1,6]上取值,求满足a·b<0的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅行社为调查市民喜欢“人文景观”景点是否与年龄有关,随机抽取了55名市民,得到数据如下表:
喜欢 | 不喜欢 | 合计 | |
大于40岁 | 20 | 5 | 25 |
20岁至40岁 | 10 | 20 | 30 |
合计 | 30 | 25 | 55 |
(1)判断是否有![]() 的把握认为喜欢“人文景观”景点与年龄有关?
的把握认为喜欢“人文景观”景点与年龄有关?
(2)已知20岁到40岁喜欢“人文景观”景点的市民中,有3位还比较喜欢“自然景观”景点,现在从20岁到40岁的10位市民中,选出3名,记选出喜欢“自然景观”景点的人数为![]() ,求
,求![]() 的分布列、数学期望.
的分布列、数学期望.
(参考公式:![]() ,其中
,其中![]() )
)
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】雾霾大气严重影响人们的生活,某科技公司拟投资开发新型节能环保产品,策划部制定投资计划时,不仅要考虑可能获得的盈利,而且还要考虑可能出现的亏损,经过市场调查,公司打算投资甲、乙两个项目,根据预测,甲、乙项目可能的最大盈利率分别为![]() 和
和![]() ,可能的最大亏损率分别为
,可能的最大亏损率分别为![]() 和
和![]() ,投资人计划投资金额不超过9万元,要求确保可能的资金亏损不超过
,投资人计划投资金额不超过9万元,要求确保可能的资金亏损不超过![]() 万元.
万元.
![]() Ⅰ
Ⅰ![]() 若投资人用x万元投资甲项目,y万元投资乙项目,试写出x,y所满足的条件,并在直角坐标系内作出表示x,y范围的图形.
若投资人用x万元投资甲项目,y万元投资乙项目,试写出x,y所满足的条件,并在直角坐标系内作出表示x,y范围的图形.
![]() Ⅱ
Ⅱ![]() 根据
根据![]() 的规划,投资公司对甲、乙两个项目分别投资多少万元,才能使可能的盈利最大?
的规划,投资公司对甲、乙两个项目分别投资多少万元,才能使可能的盈利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点M是棱长为2的正方体ABCD-A1B1C1D1的棱AD的中点,点P在面BCC1B1所在的平面内,若平面D1PM分别与平面ABCD和平面BCC1B1所成的锐二面角相等,则点P到点C1的最短距离是( )
A.![]() B.
B.![]() C.1D.
C.1D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段.下表为10名学生的预赛成绩,其中有三个数据模糊.
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
立定跳远(单位:米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
30秒跳绳(单位:次) | 63 | a | 75 | 60 | 63 | 72 | 70 | a1 | b | 65 |
在这10名学生中,进入立定跳远决赛的有8人,同时进入立定跳远决赛和30秒跳绳决赛的有6人,则
(A)2号学生进入30秒跳绳决赛
(B)5号学生进入30秒跳绳决赛
(C)8号学生进入30秒跳绳决赛
(D)9号学生进入30秒跳绳决赛
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() ,侧面
,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
, ![]() 分别为
分别为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.
(Ⅰ)求证:直线![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 为
为![]() 的中点,求平面
的中点,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值;
所成锐二面角的余弦值;
(Ⅲ)设![]() ,当
,当![]() 为何值时,直线
为何值时,直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为a的正方体ABCD﹣A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E、F为CD上任意两点,且EF的长为定值,则下面的四个值中不为定值的是( )
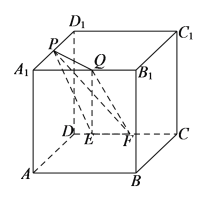
A.点P到平面QEF的距离
B.直线PQ与平面PEF所成的角
C.三棱锥P﹣QEF的体积
D.二面角P﹣EF﹣Q的大小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com