
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .过直线
.过直线![]() 的平面分别交棱
的平面分别交棱![]() ,
,![]() 于E,F两点.
于E,F两点.
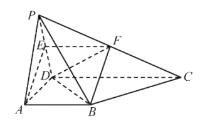
(1)求证:![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,且
,且![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)由线面平行的性质可得![]() ,取
,取![]() 中点G,连接
中点G,连接![]() ,则
,则![]() 为平行四边形,由平面几何知识
为平行四边形,由平面几何知识![]() 即
即![]() ,由线面平行的判定可得
,由线面平行的判定可得![]() 平面
平面![]() ,再由线面垂直的性质即可得证;
,再由线面垂直的性质即可得证;
(2)由题意![]() ,E、F分别为
,E、F分别为![]() 、
、![]() 的中点,建立空间直角坐标系,求出各点坐标后,进而可得平面
的中点,建立空间直角坐标系,求出各点坐标后,进而可得平面![]() 的一个法向量为
的一个法向量为![]() 、平面
、平面![]() 的一个法向量
的一个法向量![]() ,由
,由![]() 即可得解.
即可得解.
(1)证明:∵![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
又面![]() 面
面![]() ,∴
,∴![]() ,
,
取![]() 中点G,连接
中点G,连接![]() ,如图:
,如图:
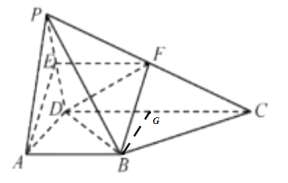
则![]() 为平行四边形,
为平行四边形,
∴![]() ,又
,又![]() ,
,![]() ,故
,故![]() ,
,
∴![]() ,∴
,∴![]() ,
,
又![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,∴
,∴![]() ;
;
(2)由(1)知![]() 平面
平面![]() ,∴
,∴![]() 即为直线
即为直线![]() 与平面
与平面![]() 所成角,
所成角,
∴![]() ,∴
,∴![]() ,解得
,解得![]() ,
,
又![]() ,∴E,F分别为
,∴E,F分别为![]() ,
,![]() 的中点,
的中点,
取![]() 中点O,连接
中点O,连接![]() ,则
,则![]() ,
,![]() ,
,
由![]() 平面
平面![]() 可得
可得![]() ,
,![]() ,故
,故![]() 平面
平面![]() ,
,
以O为原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() 轴的正方向建立空间直角坐标系,如图:
轴的正方向建立空间直角坐标系,如图:
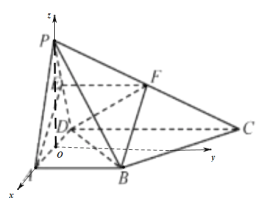
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
故![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则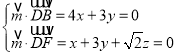 ,令
,令![]() 得
得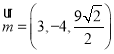 ,
,
显然![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
∴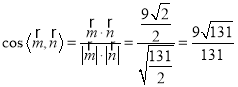 ,
,
由题知二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某市场研究人员为了了解产业园引进的甲公司前期的经营状况,对该公司2019年连续六个月的利润进行了统计,并根据得到的数据绘制了相应的折线图,如图所示:
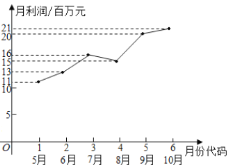
(1)由折线图可以看出,可用线性回归模型拟合月利润![]() (单位:百万元)与月份代码
(单位:百万元)与月份代码![]() 之间的关系,求
之间的关系,求![]() 关于
关于![]() 的线性回归方程,并预测该公司2020年4月份的利润;
的线性回归方程,并预测该公司2020年4月份的利润;
(2)甲公司新研制了一款产品,需要采购一批新型材料,现有A,B两种型号的新型材料可供选择,按规定每种新型材料最多可使用4个月,但新材料的不稳定性会导致材料的使用寿命不同,现对A,B两种型号的新型材料对应的产品各100件进行科学模拟测试,得到两种新型材料使用寿命的频数统计如下表:

经甲公司测算平均每件新型材料每月可以带来6万元收人入,不考虑除采购成本之外的其他成本,A型号材料每件的采购成本为10万元,B型号材料每件的采购成本为12万元.假设每件新型材料的使用寿命都是整月数,且以频率作为每件新型材料使用寿命的概率,如果你是甲公司的负责人,以每件新型材料产生利润的平均值为决策依据,你会选择采购哪款新型材料?
参考数据:![]() ,
,![]() .
.
参考公式:回归直线方程![]() ,其中
,其中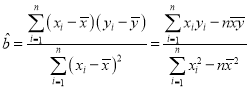 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,△PAB是边长为2的等边三角形,底面ABCD为直角梯形,AB∥CD,AB⊥BC,BC=CD=1,PD![]() .
.

(1)证明:AB⊥PD.
(2)求二面角A﹣PB﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】厂家在产品出厂前,需对产品做检验,第一次检测厂家的每件产品合格的概率为![]() ,如果合格,则可以出厂;如果不合格,则进行技术处理,处理后进行第二次检测.每件产品的合格率为
,如果合格,则可以出厂;如果不合格,则进行技术处理,处理后进行第二次检测.每件产品的合格率为![]() ,如果合格,则可以出厂,不合格则当废品回收.
,如果合格,则可以出厂,不合格则当废品回收.
![]() 求某件产品能出厂的概率;
求某件产品能出厂的概率;
![]() 若该产品的生产成本为
若该产品的生产成本为![]() 元/件,出厂价格为
元/件,出厂价格为![]() 元/件,每次检测费为
元/件,每次检测费为![]() 元/件,技术处理每次
元/件,技术处理每次![]() 元/件,回收获利
元/件,回收获利![]() 元/件.假如每件产品是否合格相互独立,记
元/件.假如每件产品是否合格相互独立,记![]() 为任意一件产品所获得的利润,求随机变量
为任意一件产品所获得的利润,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据某地区气象水文部门长期统计,可知该地区每年夏季有小洪水的概率为0.25,有大洪水的概率为0.05.
(1)从该地区抽取的![]() 年水文资料中发现,恰好3年无洪水事件的概率与恰好4年有洪水事件的概率相等,求
年水文资料中发现,恰好3年无洪水事件的概率与恰好4年有洪水事件的概率相等,求![]() 的值;
的值;
(2)今年夏季该地区某工地有许多大型设备,遇到大洪水时要损失60000元,遇到小洪水时要损失20000元.为保护设备,有以下3种方案:
方案1:修建保护围墙,建设费为3000元,但围墙只能防小洪水.
方案2:修建保护大坝,建设费为7000元,能够防大洪水.
方案3:不采取措施.
试比较哪一种方案好,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P(x0,y0)在曲线y=x2(x>0)上.已知A(0,-1),![]() ,n∈N*.记直线APn的斜率为kn.
,n∈N*.记直线APn的斜率为kn.
(1)若k1=2,求P1的坐标;
(2)若k1为偶数,求证:kn为偶数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】桂林漓江主要景点有象鼻山、伏波山、叠彩山、芦笛岩、七星岩、九马画山,小张一家人随机从这6个景点中选取2个进行游玩,则小张一家人不去七星岩和叠彩山的概率为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为提高市场销售业绩,促进某产品的销售,随机调查了该产品的月销售单价![]() (单位:元/件)及相应月销量
(单位:元/件)及相应月销量![]() (单位:万件),对近5个月的月销售单价
(单位:万件),对近5个月的月销售单价![]() 和月销售量
和月销售量![]() 的数据进行了统计,得到如下表数据:
的数据进行了统计,得到如下表数据:
月销售单价 | 9 |
| 10 |
| 11 |
月销售量 | 11 | 10 | 8 | 6 | 5 |
(Ⅰ)建立![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(Ⅱ)该公司开展促销活动,当该产品月销售单价为7元/件时,其月销售量达到18万件,若由回归直线方程得到的预测数据与此次促销活动的实际数据之差的绝对值不超过![]() 万件,则认为所得到的回归直线方程是理想的,试问:(Ⅰ)中得到的回归直线方程是否理想?
万件,则认为所得到的回归直线方程是理想的,试问:(Ⅰ)中得到的回归直线方程是否理想?
(Ⅲ)根据(Ⅰ)的结果,若该产品成本是5元/件,月销售单价![]() 为何值时(销售单价不超过11元/件),公司月利润的预计值最大?
为何值时(销售单价不超过11元/件),公司月利润的预计值最大?
参考公式:回归直线方程![]() ,其中
,其中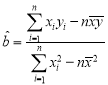 ,
,![]() .
.
参考数据:![]() ,
,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com