
【题目】某公司为提高市场销售业绩,促进某产品的销售,随机调查了该产品的月销售单价![]() (单位:元/件)及相应月销量
(单位:元/件)及相应月销量![]() (单位:万件),对近5个月的月销售单价
(单位:万件),对近5个月的月销售单价![]() 和月销售量
和月销售量![]() 的数据进行了统计,得到如下表数据:
的数据进行了统计,得到如下表数据:
月销售单价 | 9 |
| 10 |
| 11 |
月销售量 | 11 | 10 | 8 | 6 | 5 |
(Ⅰ)建立![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(Ⅱ)该公司开展促销活动,当该产品月销售单价为7元/件时,其月销售量达到18万件,若由回归直线方程得到的预测数据与此次促销活动的实际数据之差的绝对值不超过![]() 万件,则认为所得到的回归直线方程是理想的,试问:(Ⅰ)中得到的回归直线方程是否理想?
万件,则认为所得到的回归直线方程是理想的,试问:(Ⅰ)中得到的回归直线方程是否理想?
(Ⅲ)根据(Ⅰ)的结果,若该产品成本是5元/件,月销售单价![]() 为何值时(销售单价不超过11元/件),公司月利润的预计值最大?
为何值时(销售单价不超过11元/件),公司月利润的预计值最大?
参考公式:回归直线方程![]() ,其中
,其中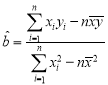 ,
,![]() .
.
参考数据:![]() ,
,
科目:高中数学 来源: 题型:
【题目】“业务技能测试”是量化考核员工绩效等级的一项重要参考依据.某公司为量化考核员工绩效等级设计了A,B两套测试方案,现各抽取![]() 名员工参加A,B两套测试方案的预测试,统计成绩(满分
名员工参加A,B两套测试方案的预测试,统计成绩(满分![]() 分),得到如下频率分布表.
分),得到如下频率分布表.
成绩频率 |
|
|
|
|
|
|
|
方案A |
|
|
|
|
|
|
|
方案B |
|
|
|
|
|
|
|
(1)从预测试成绩在![]() 的员工中随机抽取
的员工中随机抽取![]() 人,记参加方案A的人数为
人,记参加方案A的人数为![]() ,求
,求![]() 的最有可能的取值;
的最有可能的取值;
(2)由于方案A的预测试成绩更接近正态分布,该公司选择方案A进行业务技能测试.测试后,公司统计了若干部门测试的平均成绩![]() 与绩效等级优秀率
与绩效等级优秀率![]() ,如下表所示:
,如下表所示:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
根据数据绘制散点图,初步判断,选用![]() 作为回归方程.令
作为回归方程.令![]() ,经计算得
,经计算得![]() ,
,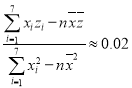 ,
,![]() .
.
(ⅰ)若某部门测试的平均成绩为![]() ,则其绩效等级优秀率的预报值为多少?
,则其绩效等级优秀率的预报值为多少?
(ⅱ)根据统计分析,大致认为各部门测试平均成绩![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,求某个部门绩效等级优秀率不低于
,求某个部门绩效等级优秀率不低于![]() 的概率为多少?
的概率为多少?
参考公式与数据:(1)![]() ,
,![]() ,
,![]() .
.
(2)线性回归方程![]() 中,
中,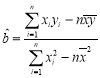 ,
,![]() .
.
(3)若随机变量![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 满足“存在正数
满足“存在正数![]() ,使得对定义域内的每一个值
,使得对定义域内的每一个值![]() ,在其定义域内都存在
,在其定义域内都存在![]() ,使
,使![]() 成立”,则称该函数为“依附函数”.
成立”,则称该函数为“依附函数”.
(1)分别判断函数①![]() ,②
,②![]() 是否为“依附函数”,并说明理由;
是否为“依附函数”,并说明理由;
(2)若函数![]() 的值域为
的值域为![]() ,求证:“
,求证:“![]() 是‘依附函数’”的充要条件是“
是‘依附函数’”的充要条件是“![]() ”.
”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为提高市场销售业绩,促进某产品的销售,随机调查了该产品的月销售单价![]() (单位:元/件)及相应月销量
(单位:元/件)及相应月销量![]() (单位:万件),对近5个月的月销售单价
(单位:万件),对近5个月的月销售单价![]() 和月销售量
和月销售量![]() 的数据进行了统计,得到如下表数据:
的数据进行了统计,得到如下表数据:
月销售单价 | 9 |
| 10 |
| 11 |
月销售量 | 11 | 10 | 8 | 6 | 5 |
(Ⅰ)建立![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(Ⅱ)该公司开展促销活动,当该产品月销售单价为7元/件时,其月销售量达到18万件,若由回归直线方程得到的预测数据与此次促销活动的实际数据之差的绝对值不超过![]() 万件,则认为所得到的回归直线方程是理想的,试问:(Ⅰ)中得到的回归直线方程是否理想?
万件,则认为所得到的回归直线方程是理想的,试问:(Ⅰ)中得到的回归直线方程是否理想?
(Ⅲ)根据(Ⅰ)的结果,若该产品成本是5元/件,月销售单价![]() 为何值时(销售单价不超过11元/件),公司月利润的预计值最大?
为何值时(销售单价不超过11元/件),公司月利润的预计值最大?
参考公式:回归直线方程![]() ,其中
,其中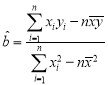 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直四棱柱![]() 中,四边形
中,四边形![]() 为梯形,
为梯形, ![]() ,且
,且![]() .过
.过![]() 三点的平面记为
三点的平面记为![]() ,
, ![]() 与
与![]() 的交点为
的交点为![]() .
.
(I)证明: ![]() 为
为![]() 的中点;
的中点;
(II)求此四棱柱被平面![]() 所分成上下两部分的体积之比.
所分成上下两部分的体积之比.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是单调递增的等差数列,a2+a4=14且a2﹣1,a3+1,a4+7成等比数列.
(1)求数列{an}的通项公式;
(2)设数列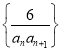 的前n项和为Sn.
的前n项和为Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动圆![]() 过定点
过定点![]() ,且在
,且在![]() 轴上截得的弦
轴上截得的弦![]() 的长为4.
的长为4.
(1)若动圆圆心![]() 的轨迹为曲线
的轨迹为曲线![]() ,求曲线
,求曲线![]() 的方程;
的方程;
(2)在曲线![]() 的对称轴上是否存在点
的对称轴上是否存在点![]() ,使过点
,使过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 的交点
的交点![]() 满足
满足![]() 为定值?若存在,求出点
为定值?若存在,求出点![]() 的坐标及定值;若不存在,请说明理由.
的坐标及定值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com