
分析 根据题意,解方程x2-2x-3=0可得集合M={-1,3},进而对P分三种情况讨论:①、若P=∅,即方程ax-1=0无解,分析可得a的值;②、若P={-1},即方程ax-1=0的解为x=-1,分析可得a的值;③、若P={3},同理可得方程ax-1=0的解为x=3,分析可得a的值;综合三种情况可得答案.
解答 解:根据题意,集合M={x|x2-2x-3=0}={-1,3},
若P?M,则分3种情况讨论:
①、若P=∅,即方程ax-1=0无解,则a=0;
②、若P={-1},即方程ax-1=0的解为x=-1,则有-a-1=0,解可得a=-1;
③、若P={3},即方程ax-1=0的解为x=3,则有3a-1=0,解可得a=$\frac{1}{3}$;
则a可取的值为0、-1、$\frac{1}{3}$,
故实数a的取值集合为{0,-1,$\frac{1}{3}$}.
点评 本题考查集合的子集运算,容易忽略P为空集的情况.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
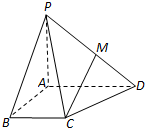 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面为直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面为直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
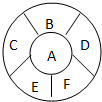 如图、用四种不同的颜色给标有字母的6个区域染色,要求相邻的区域不能染同色,则不同的染色方法有( )
如图、用四种不同的颜色给标有字母的6个区域染色,要求相邻的区域不能染同色,则不同的染色方法有( )| A. | 720种 | B. | 240种 | C. | 120种 | D. | 96种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com