
| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | 2 | D. | 4 |
分析 求出$\overrightarrow{a}•\overrightarrow{b}$及|$\overrightarrow{a}$|,计算($\overrightarrow{a}-2\overrightarrow{b}$)2的数值再开方即可.
解答 解:|$\overrightarrow{a}$|=2,$\overrightarrow{a}•\overrightarrow{b}$=|$\overrightarrow{a}$||$\overrightarrow{b}$|cos$\frac{π}{3}$=1,
∴($\overrightarrow{a}-2\overrightarrow{b}$)2=${\overrightarrow{a}}^{2}$-4$\overrightarrow{a}•\overrightarrow{b}$+4${\overrightarrow{b}}^{2}$=4.
∴|$\overrightarrow{a}$-2$\overrightarrow{b}$|=2.
故选C.
点评 本题考查了平面向量的数量积运算,属于基础题.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{4}$ | B. | -$\frac{1}{8}$ | C. | -$\frac{\sqrt{3}}{8}$ | D. | -$\frac{3}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | 3 | 4 | 5 | 6 |
| y | $\frac{5}{2}$ | m | 4 | $\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,3} | B. | {1,3,4} | C. | {1,4,5} | D. | {2,3,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
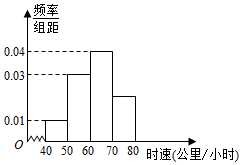 已知某一段公路限速70公里/小时,现抽取400辆通过这一段公路的汽车的时速,其频率分布直方图如图所示,则这400辆汽车中在该路段超速的有80辆.
已知某一段公路限速70公里/小时,现抽取400辆通过这一段公路的汽车的时速,其频率分布直方图如图所示,则这400辆汽车中在该路段超速的有80辆.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com