
【题目】如图,设抛物线![]() 与
与![]() 的公共点
的公共点![]() 的横坐标为
的横坐标为![]() ,过
,过![]() 且与
且与![]() 相切的直线交
相切的直线交![]() 于另一点
于另一点![]() ,过
,过![]() 且与
且与![]() 相切的直线交
相切的直线交![]() 于另一点
于另一点![]() ,记
,记![]() 为
为![]() 的面积.
的面积.
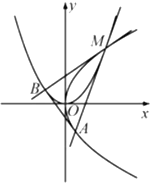
(Ⅰ)求![]() 的值(用
的值(用![]() 表示);
表示);
(Ⅱ)若![]() ,求
,求![]() 的取值范围.
的取值范围.
注:若直线与抛物线有且只有一个公共点,且与抛物线的对称轴不平行也不重合,则称该直线与抛物线相切.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]()
【解析】
(Ⅰ)将![]() 的横坐标为
的横坐标为![]() 代入抛物线
代入抛物线![]() 解析式可得
解析式可得![]() ,再代入抛物线
,再代入抛物线![]() 解析式,化简即可用
解析式,化简即可用![]() 表示
表示![]() 的值.
的值.
(Ⅱ)设出点![]() 的坐标,结合M的坐标即可表示出直线
的坐标,结合M的坐标即可表示出直线![]() 的方程.联立抛物线
的方程.联立抛物线![]() ,根据相切时判别式
,根据相切时判别式![]() 可得
可得![]() ,表示出直线
,表示出直线![]() 的方程.利用两点式表示出直线
的方程.利用两点式表示出直线![]() 的斜率,即可用
的斜率,即可用![]() 表示出点
表示出点![]() 的坐标.同理可求得
的坐标.同理可求得![]() 点的坐标.进而利用两点间距离公式表示出
点的坐标.进而利用两点间距离公式表示出![]() ,利用点到直线距离公式求得
,利用点到直线距离公式求得![]() 到直线
到直线![]() 的距离,即可表示出
的距离,即可表示出![]() 的面积
的面积![]() .结合
.结合![]() 的取值范围,即可求得
的取值范围,即可求得![]() 的取值范围.
的取值范围.
(Ⅰ)因点![]() 在抛物线
在抛物线![]() :
:![]() 上,故
上,故![]()
又点![]() 在抛物线
在抛物线![]() :
:![]() 上,故
上,故![]() ,
,
则![]()
(Ⅱ)设点![]() ,直线
,直线![]() 的方程为
的方程为![]()
联立方程组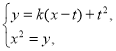 消去
消去![]() ,得
,得![]()
则![]()
因此![]()
即直线![]() 的方程为
的方程为![]()
则直线![]() 的斜率
的斜率
从而![]() ,即
,即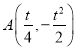
同理,直线![]() 的方程为
的方程为![]() ,点
,点
因此
点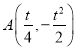 到直线
到直线![]() :
:![]() 的距离
的距离
故![]() 的面积
的面积
即![]()
因为![]()
即![]()
解得![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 的极坐标为
的极坐标为![]() .
.
(1)求![]() 的直角坐标方程和
的直角坐标方程和![]() 的直角坐标;
的直角坐标;
(2)设![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着社会的进步,经济的发展,道路上的汽车越来越多,随之而来的交通事故也增多.据有关部门调查,发生车祸的驾驶员中尤其是21 岁以下年轻人所占比例居高,因此交通管理有关部门,对2018 年参加驾照考试的21 岁以下学员随机抽取10 名学员,对他们参加的科目三(道路驾驶)和科目四(安全文明驾驶相关知识)进行两轮现场测试,并把两轮测试成绩的平均分作为该名学员的抽测成绩.记录的数据如下:
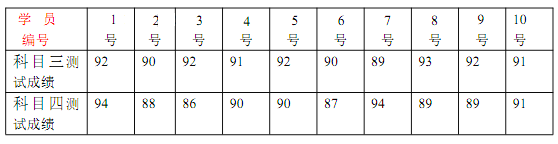
(1)从2018年参加驾照考试的21岁以下学员中随机选取一名学员,试估计这名学员抽测成绩大于或等于90分的概率;
(2)根据规定,科目三和科目四测试成绩均达到90分以上(含90)才算测试合格.
(i)从抽测的1号至5号学员中任取两名学员,记![]() 为学员测试合格的人数,求
为学员测试合格的人数,求![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(ii) 记抽取的10名学员科目三和科目四测试成绩的方差分别为![]() ,
,![]() ,试比较
,试比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线![]() 的左、右焦点为
的左、右焦点为![]() ,
,![]() ,
,![]() 为
为![]() 右支上的动点(非顶点),
右支上的动点(非顶点),![]() 为
为![]() 的内心.当
的内心.当![]() 变化时,
变化时,![]() 的轨迹为( )
的轨迹为( )
A.直线的一部分B.椭圆的一部分
C.双曲线的一部分D.无法确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信运动是由腾讯开发的一个类似计步数据库的公众账号,很多手机用户加入微信运动后,为了让自己的步数能领先于朋友,运动的积极性明显增强.微信运动公众号为了解用户的一些情况,在微信运动用户中随机抽取了100名用户,统计了他们某一天的步数,数据整理如下:
|
|
|
|
|
|
|
|
| 5 | 20 | 50 | 18 | 3 | 3 | 1 |
(Ⅰ)根据表中数据,在如图所示的坐标平面中作出其频率分布直方图,并在纵轴上标明各小长方形的高;
(Ⅱ)若视频率分布为概率分布,在微信运动用户中随机抽取3人,求至少2人步数多于1.2万步的概率;
(Ⅲ)若视频率分布为概率分布,在微信运动用户中随机抽取2人,其中每日走路不超过0.8万步的有![]() 人,超过1.2万步的有
人,超过1.2万步的有![]() 人,设
人,设![]() ,求的分布列及数学期望.
,求的分布列及数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为矩形,侧面
为矩形,侧面![]() 底面
底面![]() ,
,![]() 为棱
为棱![]() 的中点,
的中点,![]() 为棱
为棱![]() 上任意一点,且不与
上任意一点,且不与![]() 点、
点、![]() 点重合.
点重合.![]() .
.
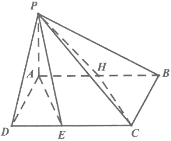
(1)求证:平面![]() 平面
平面![]() ;
;
(2)是否存在点![]() 使得平面
使得平面![]() 与平面
与平面![]() 所成的角的余弦值为
所成的角的余弦值为![]() ?若存在,求出点
?若存在,求出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
某学校高一数学兴趣小组对学生每周平均体育锻炼小时数与体育成绩优秀(体育成绩满分100分,不低于85分称优秀)人数之间的关系进行分析研究,他们从本校初二,初三,高一,高二,高三年级各随机抽取了40名学生,记录并整理了这些学生周平均体育锻炼小时数与体育成绩优秀人数,得到如下数据表:
初二 | 初三 | 高一 | 高二 | 高三 | |
周平均体育锻炼小时数工(单位:小时) | 14 | 11 | 13 | 12 | 9 |
体育成绩优秀人数y(单位:人) | 35 | 26 | 32 | 26 | 19 |
该兴趣小组确定的研究方案是:先从这5组数据中选取3组数据求线性回归方程,再用剩下的2组数据进行检验.
(1)若选取的是初三,高一,高二的3组数据,请根据这3组数据,求出y关于x的线性回归方程![]() ;
;
(2)若由线性回归方程得到的估计数据与所选取的检验数据的误差均不超过1,则认为得到的线性回归方程是可靠的,试问(1)中所得到的线性回归方程是否可靠?
参考数据:![]() ,
,![]() .
.
参考公式: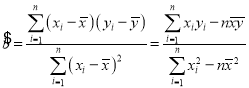 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆E:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,且椭圆E的短轴的端点到焦点的距离等于2.
,且椭圆E的短轴的端点到焦点的距离等于2.
(1)求椭圆E的标准方程;
(2)己知A,B分别为椭圆E的左、右顶点,过x轴上一点P(异于原点)作斜率为k(k≠0)的直线l与椭圆E相交于C,D两点,且直线AC与BD相交于点Q.①若k=1,求线段CD中点横坐标的取值范围;②判断![]() 是否为定值,并说明理由.
是否为定值,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com