
分析 (1)直接利用平方关系求得sinx的值;
(2)利用同角三角函数基本关系式及倍角公式求得tan2x,再由两角和的正切得答案.
解答 解:(1)∵x∈($\frac{π}{2},π$),
∴sinx=$\sqrt{1-co{s}^{2}x}=\sqrt{1-(-\frac{\sqrt{2}}{10})^{2}}=\frac{7\sqrt{2}}{10}$;
(2)由(1)得sinx=$\frac{7\sqrt{2}}{10}$,
∴$tanx=\frac{sinx}{cosx}=-7$,
则tan2x=$\frac{2tanx}{1-ta{n}^{2}x}=\frac{2×(-7)}{1-(-7)^{2}}=\frac{7}{24}$.
∴$tan(2x+\frac{π}{4})=\frac{tan2x+tan\frac{π}{4}}{1-tan2xtan\frac{π}{4}}$=$\frac{\frac{7}{24}+1}{1-\frac{7}{24}}=\frac{31}{17}$.
点评 本题考查两角和与差的正切函数,考查了同角三角函数基本关系式的应用,是基础题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
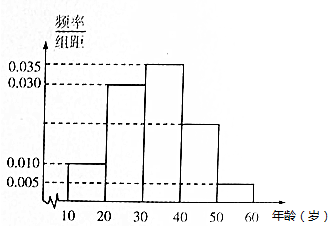 为了调查市民对某活动的认可程度,研究人员对其所在地区年龄在10~60岁间的n位市民作出调查,并将统计结果绘制成频率分布直方图如图所示,若被调查的年龄在20~30岁间的市民有480人,则可估计被调查的年龄在40~50岁间的市民有320人.
为了调查市民对某活动的认可程度,研究人员对其所在地区年龄在10~60岁间的n位市民作出调查,并将统计结果绘制成频率分布直方图如图所示,若被调查的年龄在20~30岁间的市民有480人,则可估计被调查的年龄在40~50岁间的市民有320人.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
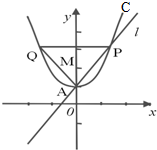 已知二次函数y=ax2+1的图象为抛物线C,过顶点A(0,1)的直线l与抛物线C相交于另外一点P,点Q为抛物线C上另外一点,且点M(0,m)到直线l的距离为1.
已知二次函数y=ax2+1的图象为抛物线C,过顶点A(0,1)的直线l与抛物线C相交于另外一点P,点Q为抛物线C上另外一点,且点M(0,m)到直线l的距离为1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 64 | B. | 100 | C. | 36 | D. | 136 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com