练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】对于定义在上的函数，有下述命题：①若是奇函数，则的图象关于点对称；②函数的图象关于直线对称，则为偶函数；③若对，有，则2是的一个周期；④函数与的图象关于直线对称.其中正确的命题是______.（写出所有正确命题的序号）

    【答案】①②③④

    【解析】

    ①根据奇函数定义分析；②根据偶函数定义分析；③根据周期函数的定义分析；④根据函数的对称性分析.

    ①：是奇函数的图象关于点成中心对称的图象关于点成中心对称，故正确；

    ②：是偶函数的图象关于直线对称的图象关于直线对称，故正确；

    ③：因为，所以，所以，所以，由此可知是的一个周期，故正确；

    ④：因为的图象与的图象关于对称，的图象是由的图象向右移动个单位得到的，的图象是由的图象向右移动个单位得到的，所以函数与的图象关于直线对称，故正确.

    故答案为：①②③④.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

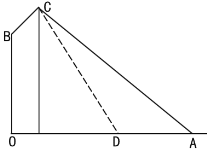
    【题目】如图，在路边安装路灯：路宽米，灯杆长米，且与灯柱成120°角，路灯采用锥形灯罩，灯罩轴线与灯杆垂直且正好通过道路路面的中线.

    （1）求灯柱高的长度（精确到0.01米）；

    （2）若该路灯投射出的光成一个圆锥体，该圆锥体母线与轴线的夹角是30°，写出路灯在路面上投射出的截面图形的边界是什么曲线？写出其相应的几何量（精确到0.01米）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知某圆的极坐标方程为，求

    (1)圆的普通方程和参数方程；

    (2)圆上所有点中的最大值和最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆:的上顶点为A,以A为圆心，椭圆的长半轴为半径的圆与y轴的交点分别为、.

    （1）求椭圆的方程；

    （2）设不经过点A的直线与椭圆交于P、Q两点，且,试探究直线是否过定点？若过定点，求出该定点的坐标，若不过定点，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

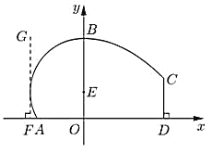
    【题目】某地拟建造一座体育馆，其设计方案侧面的外轮廓线如图所示：曲线是以点为圆心的圆的一部分，其中，是圆的切线，且，曲线是抛物线的一部分，，且恰好等于圆的半径.

    （1）若米，米，求与的值；

    （2）若体育馆侧面的最大宽度不超过75米，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知两个不相等的非零向量，，两组向量，，，，和，，，，，均由2个和3个排列而成，记，表示S所有可能取值中的最小值，则下列命题正确的是________．（写出所有正确命题的编号）

    ①S有5个不同的值；②若，则与无关；③若，则与无关；④若，则；⑤若，，则与的夹角为.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点在抛物线上，则当点到点的距离与点到抛物线焦点距离之和取得最小值时，点的坐标为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

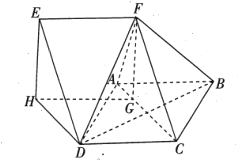
    【题目】如图，四边形是边长为2的菱形，且.四边形是平行四边形，且.点，在平面内的射影为，，且在上，四棱锥的体积为2.

    （1）求证：平面平面；

    （2）在上是否存在点，使平面？如果存在，是确定点的位置，如果不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】据历史记载，美日在中途岛(Midway)海战前，美方截获了日方密码电报，据美方已破译的密码得知，日方将向某岛进行军事活动，但关键含有地点的部分却被日方换成了另一种密码．经专家研究，估计是一种密匙密码，且密匙为3位．所谓密匙密码是指：将一段英文字母的明文(未加密前原文)经过对某一组数字(即密匙)的变换，改变成了另一组英文字母成为密文(加密后的文字)例如：明文： (不计空格，不计大小写)在密匙为：1 9 2的条件下，变换过程如下图所示：

    s

    t

    u

    d

    e

    n

    t

    1

    9

    2

    1

    9

    2

    1

    t

    c

    w

    e

    n

    p

    u

    则密文为：，试根据上面信息回答下面问题：

    （1）在密匙为111的条件下，填写下表，并写出密文；

    s

    t

    u

    d

    e

    n

    t

    密文____________________．

    （2）若请填写下表，并写出密匙；

    s

    t

    u

    d

    e

    n

    t

    密匙为_____________．

    （3)若下面即是那段包含地点(Midway)的破译不出的密文：,且此段密文也是3位密匙加密，试填写下表，写出密匙，并将此段密文翻译成明文．（不必证明，写出明文即可）

    c

    w

    b

    c

    f

    s

    o

    l

    l

    y

    d

    g

    密匙为___________，明文为_________．

    查看答案和解析>>

    同步练习册答案