Question

【题目】如图，在四棱锥P一ABCD中，已知，点Q为AC中点，底面ABCD,，点M为PC的中点.

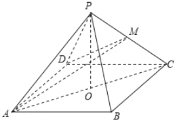
（1）求直线PB与平面ADM所成角的正弦值；

（2）求二面角D-AM-C的正弦值；

（3）记棱PD的中点为N，若点Q在线段OP上，且平面ADM，求线段OQ的长.

Answer 1

【答案】（1）；（2）；（3）.

【解析】

以O为原点，分别以向量的方向为x轴,y轴,z轴正方向，可以建立空间直角坐标系，（1）求出直线PB的方向向量，利用向量垂直数量积为零列方程求出平面ADM的法向量，可求直线PB与平面ADM所成角的正弦值；（2）由已知可得平面，故是平面的一个法向量，结合（1）中平面ADM的法向量，利用空间向量夹角余弦公式可求二面角D-AM-C的余弦值，从而可得正弦值；（3）设线段OQ的长为，则点Q的坐标为，由已知可得点N的坐标为，利用直线与平面的法向量数量积为零列方程求解即可.

依题意，以O为原点，分别以向量的方向为x轴,y轴,z轴正方向，可以建立空间直角坐标系（如图），可得，

.

（1）依题意，可得，

设为平面ADM的法向量，则，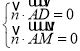

即，不妨设，可得，

又， 故，

直线PB与平面ADM所成角的正弦值为；

（2）由已知可得，

所以平面，

故是平面的一个法向量，

依题意可得，

因此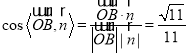有，于是有，

二面角D-AM-C的正弦值；

（3）设线段OQ的长为，则点Q的坐标为，

由已知可得点N的坐标为，进而可得，

由平面ADM，故，

即，解得，

线段OQ的长为.