
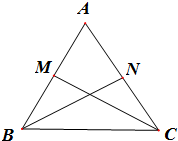
 在△ABC中,AB=4,AC=3,M,N分别是AB,AC的中点.
在△ABC中,AB=4,AC=3,M,N分别是AB,AC的中点.| AB |
| AC |
| BN |
| CM |
| BN |
| CM |
| BN |
| CM |
| π |
| 3 |
| BN |
| CM |
| BN |
| BA |
| AN |
| AB |
| 1 |
| 2 |
| AC |
| CM |
| AM |
| AC |
| 1 |
| 2 |
| AB |
| AC |
| AB |
| AC |
| AB |
| AC| |
| BN |
| CM |
| AB |
| 1 |
| 2 |
| AC |
| 1 |
| 2 |
| AB |
| AC |
| 5 |
| 4 |
| AB |
| AC |
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
| AC |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| BN |
| CM |
| 5 |
| 4 |
| AB |
| AC |
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
| AC |
| BN |
| CM |
| BN |
| CM |
| 5 |
| 4 |
| AB |
| AC |
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
| AC |
| AB |
| AC |
| 5 |
| 6 |
| ||
| 6 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 5 |
| 6 |
| 1 |
| 2 |
| ||
| 6 |
| ||
| 2 |
5-
| ||
| 12 |


科目:高中数学 来源: 题型:
| 1 |
| 2 |
| f(x 2)-f(x1) |
| x2-x1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
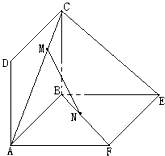
 在刚刚结束的校运会中,学校要求高一年级全体在篮球场观看比赛,如图所示,某同学为了拍摄下本班同学100m短跑的全过程,希望拍摄点P与100米的起点A,终点B的张角最大,现做如下数学模型:记百米跑道为4个单位(每单位25米),终点B离观赛区直线l距离为1单位,每个班的间距为1单位,如图所示,问该同学最好到哪个班所在的区域拍摄( )
在刚刚结束的校运会中,学校要求高一年级全体在篮球场观看比赛,如图所示,某同学为了拍摄下本班同学100m短跑的全过程,希望拍摄点P与100米的起点A,终点B的张角最大,现做如下数学模型:记百米跑道为4个单位(每单位25米),终点B离观赛区直线l距离为1单位,每个班的间距为1单位,如图所示,问该同学最好到哪个班所在的区域拍摄( )| A、12班 | B、11班 |
| C、10班 | D、9班 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2nπ |
| 3 |
| S3n |
| n•2n-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| e |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com