Question

9．等腰直角三角形ABC中，AB=AC=4，且2$\overrightarrow{AE}$=$\overrightarrow{EC}$，$\overrightarrow{BD}$=$\overrightarrow{DC}$，则$\overrightarrow{BE}$•$\overrightarrow{AD}$=-$\frac{16}{3}$．

Answer 1

分析 求得$\overrightarrow{AB}$•$\overrightarrow{AC}$=0，由中点向量表示和向量共线，$\overrightarrow{BE}$、$\overrightarrow{AD}$统一成$\overrightarrow{AB}$、$\overrightarrow{AC}$表示，再由向量数量积的性质：向量的平方即为模的平方，计算即可得到所求值．

解答 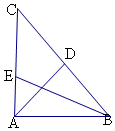解：$\overrightarrow{AB}$•$\overrightarrow{AC}$=4×4×cos90°=0，
2$\overrightarrow{AE}$=$\overrightarrow{EC}$，$\overrightarrow{BD}$=$\overrightarrow{DC}$，
则$\overrightarrow{BE}$•$\overrightarrow{AD}$=（$\overrightarrow{AE}$-$\overrightarrow{AB}$）•$\frac{1}{2}$（$\overrightarrow{AB}$+$\overrightarrow{AC}$）
=（$\frac{1}{3}$$\overrightarrow{AC}$-$\overrightarrow{AB}$）•$\frac{1}{2}$（$\overrightarrow{AB}$+$\overrightarrow{AC}$）
=$\frac{1}{6}$$\overrightarrow{AC}$²-$\frac{1}{2}$$\overrightarrow{AB}$²-$\frac{1}{3}$$\overrightarrow{AB}$•$\overrightarrow{AC}$
=$\frac{1}{6}$×16-$\frac{1}{2}$×16=-$\frac{16}{3}$．
故答案为：-$\frac{16}{3}$．

点评 本题考查向量数量积的定义和性质，主要是向量的平方即为模的平方，以及中点向量表示，向量共线等，考查运算能力，属于中档题．