
【题目】若函数![]() 满足:对于任意正数
满足:对于任意正数![]() ,
,![]() ,都有
,都有![]() ,
,![]() ,且
,且![]() ,则称函数
,则称函数![]() 为“速增函数”.
为“速增函数”.
(1)试判断函数![]() 与
与![]() 是否是“速增函数”;
是否是“速增函数”;
(2)若函数![]() 为“速增函数”,求
为“速增函数”,求![]() 的取值范围;
的取值范围;
(3)若函数![]() 为“速增函数”,且
为“速增函数”,且![]() ,求证:对任意
,求证:对任意![]() ,都有
,都有![]() .
.
【答案】(1)![]() 是,
是,![]() 不是;(2)
不是;(2)![]() ;(3)证明见解析
;(3)证明见解析
【解析】
(1)![]() 根据定义进行判断即可,
根据定义进行判断即可,![]() 利用特殊值,举出反例;
利用特殊值,举出反例;
(2)根据定义可知![]() ,即
,即![]() 对一切正数
对一切正数![]() 恒成立,可得
恒成立,可得![]() ,由
,由![]() ,可得
,可得
![]() 得出
得出![]() ,最后求出
,最后求出![]() 的范围;
的范围;
(3)根据定义,令![]() ,可知
,可知![]() ,即
,即![]() ,故对于正整数
,故对于正整数![]() 与正数
与正数![]() ,都有
,都有![]() ,进而得出结论.
,进而得出结论.
(1)对于函数![]() ,当
,当![]() ,
,![]() 时,
时,![]() ,
,
又![]() ,
,
所以![]() ,
,
故![]() 是“速增函数”.
是“速增函数”.
对于函数![]() ,当
,当![]() 时,
时,![]() ,
,
故![]() 不是“速增函数”.
不是“速增函数”.
(2)当![]() ,
,![]() 时,由
时,由![]() 是“速增函数”,
是“速增函数”,
可知![]() ,即
,即![]() 对一切正数
对一切正数![]() 恒成立,
恒成立,
又![]() ,可得
,可得![]() 对一切正数
对一切正数![]() 恒成立,所以
恒成立,所以![]() .
.
由![]() ,可得
,可得![]() ,
,
即![]()
![]() ,
,
故![]() ,又
,又![]() ,故
,故![]() ,
,
由![]() 对一切正数
对一切正数![]() ,
,![]() 恒成立,可得
恒成立,可得![]() ,即
,即![]() .
.
综上可知,![]() 的取值范围是
的取值范围是![]() .
.
(3)由函数![]() 为“速增函数”,可知对于任意正数
为“速增函数”,可知对于任意正数![]() ,
,![]() ,
,
都有![]() ,
,![]() ,且
,且![]() ,
,
令![]() ,可知
,可知![]() ,即
,即![]() ,
,
故对于正整数![]() 与正数
与正数![]() ,都有
,都有![]() ,
,
对任意![]() ,
,![]() ,可得
,可得![]() ,又
,又![]() ,
,
所以![]() ,
,
同理![]() ,
,
故![]() .
.


科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() 若满足:①对任意
若满足:①对任意![]() 、
、![]() ,都有
,都有![]() ;②对任意
;②对任意![]() ,都有
,都有![]() ,则称函数
,则称函数![]() 为“中心捺函数”,其中点
为“中心捺函数”,其中点![]() 称为函数
称为函数![]() 的中心.已知函数
的中心.已知函数![]() 是以
是以![]() 为中心的“中心捺函数”,若满足不等式
为中心的“中心捺函数”,若满足不等式![]() ,当
,当![]() 时,
时,![]() 的取值范围为( )
的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某射击小组有甲、乙、丙三名射手,已知甲击中目标的概率是![]() ,甲、丙二人都没有击中目标的概率是
,甲、丙二人都没有击中目标的概率是![]() ,乙、丙二人都击中目标的概率是
,乙、丙二人都击中目标的概率是![]() .甲乙丙是否击中目标相互独立.
.甲乙丙是否击中目标相互独立.
(1)求乙、丙二人各自击中目标的概率;
(2)设乙、丙二人中击中目标的人数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在![]() 上的函数
上的函数![]() ,若存在正常数
,若存在正常数![]() 、
、![]() ,使得
,使得![]() 对一切
对一切![]() 均成立,则称
均成立,则称![]() 是“控制增长函数”.在以下四个函数中:①
是“控制增长函数”.在以下四个函数中:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .是“控制增长函数”的有( )个
.是“控制增长函数”的有( )个
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了丰富学生活动,在体育课上,体育教师设计了一个游戏,让甲、乙、丙三人各抓住橡皮带的一端,甲站在直角![]() 斜边
斜边![]() 的中点
的中点![]() 处,乙站在
处,乙站在![]() 处,丙站在
处,丙站在![]() 处.游戏开始,甲不动,乙、丙分别以
处.游戏开始,甲不动,乙、丙分别以![]() 和
和![]() 的速度同时出发,匀速跑向终点
的速度同时出发,匀速跑向终点![]() 和
和![]() ,运动过程中绷紧的橡皮带围成一个如图所示的
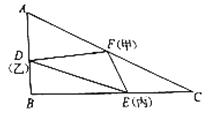
,运动过程中绷紧的橡皮带围成一个如图所示的![]() .(规定:只要有一人跑到终点,游戏就结束,且
.(规定:只要有一人跑到终点,游戏就结束,且![]() ).已知
).已知![]() 长为
长为![]() ,
,![]() 长为
长为![]() ,记经过
,记经过![]() 后
后![]() 的面积为
的面积为![]() .
.
(1)求![]() 关于
关于![]() 的函数表示,并求出
的函数表示,并求出![]() 的取值范围;
的取值范围;
(2)当游戏进行到![]() 时,体育教师宣布停止,求此时
时,体育教师宣布停止,求此时![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com