
分析 (1)根据AF2,AB,BF2成等差数列,可得2AB=AF2+BF2,利用椭圆定义可得AB=$\frac{4a}{3}$.设l:x=y-c,代入椭圆C的方程,整理得(a2+b2)y2-2b2cy-b4=0,利用根与系数的关系化简可得a=$\sqrt{2}$b,从而求得椭圆的离心率;
(2)设AB的中点为N(x0,y0),运用中点坐标公式,可得N的坐标,根据PA=PB知PM为AB的中垂线,可得kPN=-1,从而可求b=6,进而可求椭圆E的方程.
解答 解:(1)∵AF2,AB,BF2成等差数列,
∴2AB=AF2+BF2,
由椭圆定义可得,AB+AF2+BF2=4a,
∴AB=$\frac{4}{3}a$,
设A(x1,y1),B(x2,y2),F1(-c,0),l:x=y-c,
代入椭圆C的方程,整理得(a2+b2)y2-2b2cy-b4=0,①
则AB2=(x1-x2)2+(y1-y2)2=2(y1-y2)2=2[(y1+y2)2-4y1y2]
=2[($\frac{2{b}^{2}c}{{a}^{2}+{b}^{2}}$)2+$\frac{4{b}^{4}}{{a}^{2}+{b}^{2}}$]=$\frac{8{b}^{4}}{({a}^{2}+{b}^{2})^{2}}$•2a2,
化简得a=$\sqrt{2}$b.
∴椭圆的离心率e=$\frac{c}{a}$=$\sqrt{\frac{{c}^{2}}{{a}^{2}}}=\sqrt{\frac{{a}^{2}-{b}^{2}}{{a}^{2}}}=\sqrt{\frac{{b}^{2}}{2{b}^{2}}}=\frac{\sqrt{2}}{2}$;
(2)设AB的中点为N(x0,y0),由(1)可得,
x0=$\frac{{x}_{1}+{x}_{2}}{2}$=$\frac{{b}^{2}c}{{a}^{2}+{b}^{2}}$-c=$\frac{c}{3}-c=-\frac{2c}{3}$,y0=x0+c=$\frac{c}{3}$,
由PA=PB,可得kPN=-1,即$\frac{{y}_{0}}{{x}_{0}+2}=-1$,
化简为$\frac{c}{3}=\frac{2c}{3}-2$,解得c=6,a=6$\sqrt{2}$,b=6.
∴椭圆的方程为$\frac{{x}^{2}}{72}+\frac{{y}^{2}}{36}=1$.
点评 本题考查椭圆的标准方程,考查椭圆的简单性质,考查等差数列的性质、两点间的距离公式的应用,关键是利用PA=PB得kPN=-1,属于中档题.


科目:高中数学 来源: 题型:解答题
 如图,已知菱形ABEF所在的平面与△ABC所在的平面相互垂直,AB=4,BC=$\sqrt{6}$,BC⊥BE,∠ABE=$\frac{π}{3}$.
如图,已知菱形ABEF所在的平面与△ABC所在的平面相互垂直,AB=4,BC=$\sqrt{6}$,BC⊥BE,∠ABE=$\frac{π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
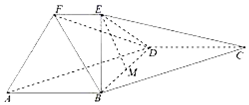 在如图所示的几何体中,四边形ABCD为平行四边形,∠ABD=90°,EB⊥面ABCD,EF∥AB,AB=2,EB=$\sqrt{3}$的中点.
在如图所示的几何体中,四边形ABCD为平行四边形,∠ABD=90°,EB⊥面ABCD,EF∥AB,AB=2,EB=$\sqrt{3}$的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是某年青年歌手大奖赛中,七位评委为甲、乙两名选手打出的分数的茎叶图(其中m为数字0~9中的一个).去掉一个最高分和一个最低分后,甲、乙两名选手得分的平均数分别为a1,a2,则一定有( )
如图是某年青年歌手大奖赛中,七位评委为甲、乙两名选手打出的分数的茎叶图(其中m为数字0~9中的一个).去掉一个最高分和一个最低分后,甲、乙两名选手得分的平均数分别为a1,a2,则一定有( )| A. | a1>a2 | B. | a1<a2 | ||
| C. | a1=a2 | D. | a1,a2的大小与m的值有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3x-4y+5=0 | B. | 3x-4y-1=0. | C. | 4x-3y-5=0 | D. | 4x-3y+5=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com