
【题目】微信是腾讯公司推出的一种手机通讯软件,它支持发送语音短信、视频、图片和文字,一经推出便风靡全国,甚至涌现出一批在微信的朋友圈内销售商品的人(被称为微商).为了调查每天微信用户使用微信的时间,某经销化妆品的微商在一广场随机采访男性、女性用户各50 名,其中每天玩微信超过6 小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有60%的把握认为“微信控”与”性别“有关?
(2)现从调查的女性用户中按分层抽样的方法选出5 人并从选出的5 人中再随机抽取3 人赠送200 元的护肤品套装,记这3 人中“微信控”的人数为X,试求X 的分布列与数学期望.
参考公式:![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
k0 | 0.455 | 0.708 | 1.323 | 3.841 | 5.024 | 6.635 |
【答案】(1)没有60%的把握(2)见解析
【解析】试题分析:(1)由列表根据公式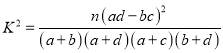 计算
计算![]() ,对照临界值表即可得出结论;(2)依题意所抽取的
,对照临界值表即可得出结论;(2)依题意所抽取的![]() 位女性中“微信控”有
位女性中“微信控”有![]() 人,得
人,得![]() 所有可能取值为
所有可能取值为![]() ,计算对应的概率,写出
,计算对应的概率,写出![]() 的分布列,由期望公式计算数学期望值.
的分布列,由期望公式计算数学期望值.
试题解析:(1)由列联表可知,
![]() =
=![]() =
=![]() ≈0.649,
≈0.649,
∵0.649<0.708,
∴没有60%的把握认为“微信控”与”性别“有关;
(2)依题意知,所抽取的5位女性中“微信控”有3人,
“非微信控”有2人,
∴X的所有可能取值为1,2,3;
且P(X=1)=![]() =
=![]() ,P(X=2)=
,P(X=2)=![]() =
=![]() ,P(X=3)=
,P(X=3)=![]() =
=![]() ,
,
∴X 的分布列为:
X | 1 | 2 | 3 |
P(X) |
|
|
|
X的数学期望为EX=1×![]() +2×
+2×![]() +3×
+3×![]() =
=![]() .
.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆E的中心在原点,离心率为 ![]() ,右焦点到直线x+y+
,右焦点到直线x+y+ ![]() =0的距离为2.
=0的距离为2.
(1)求椭圆E的方程;
(2)椭圆下顶点为A,直线y=kx+m(k≠0)与椭圆相交于不同的两点M、N,当|AM|=|AN|时,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名运动员参加“选拔测试赛”,在相同条件下,两人6次测试的成绩(单位:分)记录如下:
甲 86 77 92 72 78 84
乙 78 82 88 82 95 90
(1)用茎叶图表示这两组数据,现要从中选派一名运动员参加比赛,你认为选派谁参赛更好?说明理由(不用计算);
(2)若将频率视为概率,对运动员甲在今后三次测试成绩进行预测,记这三次成绩高于85分的次数为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() 及方差
及方差![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线C1:  ( t 为参数),曲线C2:
( t 为参数),曲线C2: ![]() (r>0,θ为参数).
(r>0,θ为参数).
(1)当r=1时,求C 1 与C2的交点坐标;
(2)点P 为曲线 C2上一动点,当r=![]() 时,求点P 到直线C1距离最大时点P 的坐标.
时,求点P 到直线C1距离最大时点P 的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC.
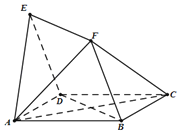
(Ⅰ)求证:AC⊥平面BDEF;
(Ⅱ)求证:FC∥平面EAD;
(Ⅲ)求二面角A﹣FC﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某险种的基本保费为![]() (单位:元),继续购买该险种的投保人称为续保人,
(单位:元),继续购买该险种的投保人称为续保人,
续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 |
|
保费 |
|
|
|
|
|
|
随机调查了该险种的400名续保人在一年内的出险情况,得到如下统计表:
出险次数 | 0 | 1 | 2 | 3 | 4 |
|
频数 | 120 | 100 | 60 | 60 | 40 | 20 |
(Ⅰ)记A为事件:“一续保人本年度的保费不高于基本保费”.求![]() 的估计值;
的估计值;
(Ⅱ)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的190%”.
求![]() 的估计值;
的估计值;
(III)求续保人本年度的平均保费估计值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各组函数中,表示同一个函数的是( )
A.y= ![]() 与y=x+1
与y=x+1
B.y=lgx与y= ![]() lgx2
lgx2
C.y= ![]() ﹣1与y=x﹣1
﹣1与y=x﹣1
D.y=x与y=logaax(a>0且a≠1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com