
分析 利用点到直线的距离公式可得l1与l2之间的距离d,设直线l与两平行直线的夹角为α,则sin$α=\frac{d}{\frac{7}{2}}$.对直线l的斜率分类讨论即可得出.
解答 解:l1与l2之间的距离$d=\frac{{|-6+\frac{5}{2}|}}{{\sqrt{{2^2}+1}}}=\frac{7}{{2\sqrt{5}}}$,
设直线l与两平行直线的夹角为α,
则$sinα=\frac{d}{{\frac{7}{2}}}=\frac{{\frac{7}{{2\sqrt{5}}}}}{{\frac{7}{2}}}=\frac{1}{{\sqrt{5}}}$,∴$cosα=\frac{2}{{\sqrt{5}}}$.
①当直线l斜率存在时,设l:y+1=kx,即l:kx-y-1=0,
则:$cosα=\frac{|2k-1|}{{\sqrt{5}\sqrt{{k^2}+1}}}=\frac{2}{{\sqrt{5}}}⇒k=-\frac{3}{4}$.
即直线l的方程为:3x+4y+4=0.
②当直线l斜率不存在时,l:x=0,$cosα=\frac{2}{{\sqrt{5}}}$符合.
所以直线l的方程为:3x+4y+4=0或x=0.
点评 本题考查了平行线之间的距离公式、分类讨论方法、直线方程、三角函数求值,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | 6 | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
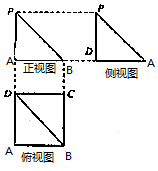 一个几何体的三视图如图所示,其中正视图和侧视图是腰长为4的两个全等的等腰直角三角形,俯视图为一个矩形与它的一条对角线.
一个几何体的三视图如图所示,其中正视图和侧视图是腰长为4的两个全等的等腰直角三角形,俯视图为一个矩形与它的一条对角线.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com