
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{2}{3}$ | D. | 1 |
分析 令PA=x(0<x<2),求出体积表达式,利用导数确定函数的单调性,求出函数的最大值.
解答 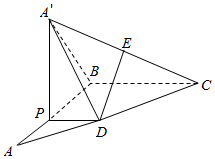 解:令PA=x(0<x<2),则A′P=PD=x.BP=2-x,因为A′P⊥PD
解:令PA=x(0<x<2),则A′P=PD=x.BP=2-x,因为A′P⊥PD
且平面A′PD⊥平面PBCD,故A′P⊥平面PBCD,
所以${V}_{{A}^{′}-PBCD}=\frac{1}{3}Sh=\frac{1}{6}(2-x)(2+x)x=\frac{1}{6}(4x-{x}^{3})$,
令f(x)=$\frac{1}{6}(4x-{x}^{3})$,由f′(x)=$\frac{1}{6}(4-3{x}^{2})\;=0$得x=$\frac{2\sqrt{3}}{3}$,
当x∈(0,$\frac{2\sqrt{3}}{3}$)时,f′(x)>0,f(x)单调递增,
当x∈($\frac{2\sqrt{3}}{3}$,2)时,f′(x)<0,f(x)单调递减,
所以,当x=$\frac{2\sqrt{3}}{3}$时,f(x)取得最大值,
即:体积最大时,PA=$\frac{2\sqrt{3}}{3}$.
故选:A
点评 本题主要考查四棱锥体积的计算,以及函数与导数的综合,根据条件求出体积的表达式,利用导数研究函数的最值是解决本题的关键.综合性较强,有一定的难度.


科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,PA⊥面ABCD,∠ABC=90°,△ABC≌△ADC,PA=AC=2AB=2,E是线段PC的中点.
如图,在四棱锥P-ABCD中,PA⊥面ABCD,∠ABC=90°,△ABC≌△ADC,PA=AC=2AB=2,E是线段PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | lg(m-n)>0 | B. | ($\frac{1}{2}$)m<($\frac{1}{2}$)n | C. | $\frac{n}{m}$<1 | D. | m2>n2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 对服务好评 | 对服务不满意 | 合计 | |
| 对商品好评 | 80 | 40 | 120 |
| 对商品不满意 | 70 | 10 | 80 |
| 合计 | 150 | 50 | 200 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|3≤x<4} | B. | {x|0≤x<3} | C. | {3} | D. | {3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0≤x≤2} | B. | {x|1≤x<2} | C. | {0,1} | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{32π}{3}$ | B. | $\frac{20\sqrt{5}π}{3}$ | C. | 8$\sqrt{6}$π | D. | 36π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com