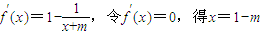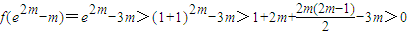设函数f(x)=x-In(x+m),其中常数m为整数.
(1)当m为何值时,f(x)≥0;
(2)定理:若函数g(x)在[a,b]上连续,且g(a)与g(b)异号,则至少存在一点x∈(a,b),使g(x)=0.
试用上述定理证明:当整数m>1时,方程f(x)=0,在[e-m-m,e2m-m]内有两个实根.
【答案】
分析:(1)求出导函数令其为0得到函数的驻点,利用导函数大于得到f(x)为增函数,小于0得到f(x)为减函数,得到函数的极小值,令f(x)的极小值≥0得到m的范围;
(2)当整数m>1时,函数f(x)在[e
-m-m,1-m]上为连续减函数,由增减性得到f(e
-m-m)与f(1-m)异号,由所给定理知,存在唯一的x
1∈(e
-m-m,1-m),使f(x
1)=0;函数f(x)在[1-m,e
-m-m]上为连续增函数且f(1-m)与f(e
2m-m)异号,由所给定理知,存在唯一的x
2∈[1-m,e
-m-m,],使f(x
2)=0,得到当整数m>1时,方程f(x)=0,在[e
-m-m,e
2m-m]内有两个实根.
解答:(1)解:函数f(x)=x-ln(x+m),x∈(-m,+∞)连续,且
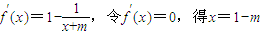
当x∈(-m,1-m)时,f’(x)<0,f(x)为减函数,f(x)>f(1-m)
当x∈(1-m,+∞)时,f’(x)>0,f(x)为增函数,f(x)>f(1-m)
根据函数极值判别方法,f(1-m)=1-m为极小值,而且
对x∈(-m,+∞)都有f(x)≥f(1-m)=1-m
故当整数m≤1时,f(x)≥1-m≥0
(2)证明:由(1)知,当整数m>1时,f(1-m)=1-m<0,函数f(x)=x-ln(x+m),在[e
-m-m,1-m]上为连续减函数.
f(e
-m-m)=e
-m-m-ln(e
-m-m+m)=e
-m>0
当整数m>1时,f(e
-m-m)与f(1-m)异号,
由所给定理知,存在唯一的x
1∈(e
-m-m,1-m),使f(x
1)=0
而当整数m>1时,
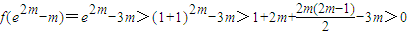
类似地,当整数m>1时,函数f(x)=x-ln(x+m),在[1-m,e
-m-m]上为连续增函数且f(1-m)与f(e
2m-m)异号,由所给定理知,存在唯一的x
2∈[1-m,e
-m-m,],使f(x
2)=0
故当m>1时,方程f(x)=0在[e
-m-m,e
2m-m]内有两个实根.
点评:考查学生利用导数研究函数极值的能力,利用给出定理证明数学题的能力.