
【题目】在①![]() ,且
,且![]() ,②
,②![]() ,且
,且![]() ,③
,③![]() ,且
,且![]() 这三个条件中任选一个,补充在下面问题中,若问题中的
这三个条件中任选一个,补充在下面问题中,若问题中的![]() 存在,求出
存在,求出![]() 和数列
和数列![]() 的通项公式与前
的通项公式与前![]() 项和;若
项和;若![]() 不存在,请说明理由.
不存在,请说明理由.
设![]() 为各项均为正数的数列
为各项均为正数的数列![]() 的前
的前![]() 项和,满足________,是否存在
项和,满足________,是否存在![]() ,使得数列
,使得数列![]() 成为等差数列?
成为等差数列?
【答案】答案不唯一,具体见解析
【解析】
由![]() ,用
,用![]() 换
换![]() 后得
后得![]() ,两式相减得
,两式相减得![]() ,若选择①,由
,若选择①,由![]() 可求得等差数列
可求得等差数列![]() 的通项公式及
的通项公式及![]() 值,前
值,前![]() 项和;若选择②,由
项和;若选择②,由![]() 得
得![]() 和
和![]() 的关系式,作为关于
的关系式,作为关于![]() 的二次方程,至少有正根,由根的分布得其条件是
的二次方程,至少有正根,由根的分布得其条件是![]() ,得出与已知矛盾的结论,说明不存在;若选择③,由
,得出与已知矛盾的结论,说明不存在;若选择③,由![]() ,同样可求
,同样可求![]() 和
和![]() .
.
解:选择①,
因为![]() ,所以
,所以![]() ,两式相减,得
,两式相减,得
![]() ,
,
即![]() ,又
,又![]() ,所以
,所以![]() ,
,
因为![]() ,且
,且![]() ,所以
,所以![]() ,
,
由![]() ,得
,得![]() ,即
,即![]() ,
,
把![]() 代入上式,得
代入上式,得![]() ,
,
当![]() 时,由
时,由![]() 及
及![]() ,得
,得![]() ,
,
所以![]() ,
,![]() ,满足
,满足![]() ,可知数列
,可知数列![]() 是以3为首项,以2为公差的等差数列.
是以3为首项,以2为公差的等差数列.
数列![]() 的通项公式为
的通项公式为![]() ,
,
数列![]() 的前
的前![]() 项和为
项和为![]() .
.
选择②,
因为![]() ,所以
,所以![]() ,两式相减,得
,两式相减,得
![]() ,
,
即![]() ,又
,又![]() ,所以
,所以![]() ,
,
由![]() ,得
,得![]() ,即
,即![]() ,
,
因为已知数列![]() 的各项均为正数,所以
的各项均为正数,所以![]() ,
,
因为关于![]() 的一元二次方程
的一元二次方程![]() 至少存在一个正实数解的充要条件是
至少存在一个正实数解的充要条件是
![]() ,
,
解得![]() ,
,
这与已知条件![]() 矛盾,所以满足条件的
矛盾,所以满足条件的![]() 不存在.
不存在.
(注:若![]() 存在两个实数解分别为
存在两个实数解分别为![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
当![]() 时,
时,![]() 的解一正一负;当
的解一正一负;当![]() 时,
时,![]() 的解一正一零;
的解一正一零;
当![]() 时,
时,![]() 的解均为正.
的解均为正.
所以方程![]() 至少存在一个正实数解,当且仅当
至少存在一个正实数解,当且仅当![]() .)
.)
选择③,因为![]() ,所以
,所以![]() ,两式相减,得
,两式相减,得
![]() ,
,
即![]() ,又
,又![]() ,所以
,所以![]() ,
,
由![]() ,得
,得![]() ,又已知
,又已知![]() ,
,
所以![]() ,
,![]() ,
,
由![]() ,得
,得![]() ,
,![]() ,所以
,所以![]() ,
,
当![]() 时,由
时,由![]() 及
及![]() 得
得![]() ,
,
由![]() ,
,![]() 及
及![]() ,得
,得![]() ,
,
所以![]() 和
和![]() 满足
满足![]() ,
,
可知数列![]() 是以3为首项,以2为公差的等差数列,
是以3为首项,以2为公差的等差数列,
数列![]() 的通项公式为
的通项公式为![]() ,
,
数列![]() 的前
的前![]() 项和为
项和为![]() .
.


科目:高中数学 来源: 题型:
【题目】《九章算术》中盈不足章中有这样一则故事:“今有良马与驽马发长安,至齐. 齐去长安三千里. 良马初日行一百九十三里,日增一十二里;驽马初日行九十七里,日减二里.” 为了计算每天良马和驽马所走的路程之和,设计框图如下图. 若输出的 ![]() 的值为 350,则判断框中可填( )
的值为 350,则判断框中可填( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产甲、乙两种产品均需用A,B两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得的最大利润为( )
甲 | 乙 | 原料限额 | |
A/吨 | 3 | 2 | 12 |
B/吨 | 1 | 2 | 8 |
A.15万元B.16万元C.17万元D.18万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个多面体的直观图及三视图如图所示,其中M ,N 分别是AF、BC 的中点
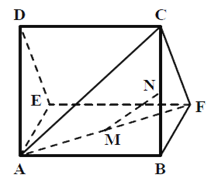
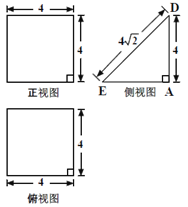
(1)求证:MN∥平面CDEF;
(2)求多面体A-CDEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对两个变量![]() 与
与![]() 进行线性相关性和回归效果分析,得到一组样本数据:
进行线性相关性和回归效果分析,得到一组样本数据:![]() 、
、![]() 、
、![]() 、
、![]() ,则下列说法不正确的是( )
,则下列说法不正确的是( )
A.残差平方和越小的模型,拟合的效果越好
B.由样本数据利用最小二乘法得到的回归方程表示的直线必过样本点的中心![]()
C.若变量![]() 与
与![]() 之间的相关系数
之间的相关系数![]() ,则变量
,则变量![]() 与
与![]() 之间具有很强的线性相关性
之间具有很强的线性相关性
D.用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 越小,说明模型的拟合效果越好
越小,说明模型的拟合效果越好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内动点![]() 与点
与点![]() ,
,![]() 连线的斜率之积为
连线的斜率之积为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() ,
,![]() 与直线
与直线![]() 分别交于
分别交于![]() ,
,![]() 两点.求证:以
两点.求证:以![]() 为直径的圆恒过定点.
为直径的圆恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆E:
中,已知椭圆E:![]() 的离心率是
的离心率是![]() ,短轴长为2,若点A,B分别是椭圆E的左右顶点,动点
,短轴长为2,若点A,B分别是椭圆E的左右顶点,动点![]() ,
,![]() ,直线
,直线![]() 交椭圆E于P点.
交椭圆E于P点.
(1)求椭圆E的方程
(2)①求证:![]() 是定值;
是定值;
②设![]() 的面积为
的面积为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com