
下列四个命题:(1)函数 在
在 时是增函数,
时是增函数, 也是增函数,所以
也是增函数,所以 是增函数;(2)若函数
是增函数;(2)若函数 与
与 轴没有交点,则
轴没有交点,则 且
且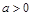 ;(3)
;(3) 的递增区间为
的递增区间为 ;(4)
;(4) 和
和 表示相等函数。
表示相等函数。
其中正确命题的个数是( )
| A.0 | B.1 | C.2 | D.3 |
A
解析试题分析:对于命题逐一的进行分析
①举一个例子y=-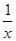 ,当x<0时,函数为增函数,当x>0时,函数为增函数,但是在x≠0时,函数不单调,所以错误;
,当x<0时,函数为增函数,当x>0时,函数为增函数,但是在x≠0时,函数不单调,所以错误;
②由若函数f(x)=ax2+bx+2与x轴没有交点,则b2-8a<0且a>0,或者b2-8a<0且a<0,或者a=b=0;所以此命题错;
③当x≥0时,y=x2-2x-3,为对称轴为直线x=1的开口向上的抛物线,所以[1,+∞)为函数的增区间;当x<0时,y=x2+2x-3,为对称轴为直线x=-1的开口向上的抛物线,所以[-1,0]为增区间,综上,y=x2-2|x|-3的递增区间为[1,+∞)和[-1,0],故③不正确;
④因为y=1+x和 =|1+x|表示的函数的解析式不同,故命题不正确.
=|1+x|表示的函数的解析式不同,故命题不正确.
故答案为A
考点:本试题主要是考查了函数单调性和函数概念,以及图像与x轴交点问题的运用。
点评:此题是一道综合题,要求学生掌握函数单调性的判断与证明和二次函数的性质,判断两个函数是否为同一函数,会利用举反例的方法说明一个命题是假命题.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:单选题
已知P:|2x-3|<1, Q:x(x-3)<0, 则P是Q的( )
| A.充分不必要条件; | B.必要不充分条件 ; |
| C.充要条件 ; | D.既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
下列有关命题的说法正确的是
A.命题“若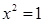 ,则 ,则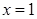 ”的否命题为“若 ”的否命题为“若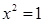 ,则 ,则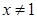 ” ” |
B.命题“若 ,则 ,则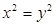 ”的逆否命题是假命题 ”的逆否命题是假命题 |
C.命题“若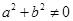 ,则 ,则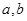 全不为0”为真命题 全不为0”为真命题 |
D.命题“若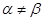 ”,则 ”,则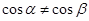 ”的逆命题为真命题 ”的逆命题为真命题 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com