
分析 (1)由a1、a4、a13成等比数列可得关于d的方程,解出d,利用等差数列的通项公式可得结果;
(2)若bn=$4+\frac{3}{2}(\frac{1}{n}-\frac{1}{n+2})$,利用裂项求和即可{bn}的前n项和Tn
解答 解:(1)由a3=7,可得a1+2d=7,
由a1,a4,a13成等比数列,且d>0,可得${a_1}({{a_1}+12d})={({{a_1}+3d})^2}$,
即2a1=3d.
解得a1=3,d=2.
所以数列{an}的通项公式为an=2n+1.
(2)由(1)知,${S_n}=\frac{{n({3+2n+1})}}{2}={n^2}+2n$,
所以${b_n}=\frac{{{a_n}{a_{n+1}}}}{S_n}$=$\frac{{({2n+1})({2n+3})}}{{n({n+2})}}=\frac{{4{n^2}+8n+3}}{{n({n+2})}}$=$4+\frac{3}{{n({n+2})}}$=$4+\frac{3}{2}(\frac{1}{n}-\frac{1}{n+2})$
所以Tn=b1+b2+b3+…+bn=$4n+\frac{3}{2}(1-\frac{1}{3}+\frac{1}{2}-\frac{1}{4}+\frac{1}{3}-\frac{1}{5}+…+\frac{1}{n}-\frac{1}{n+2})$=$4n+\frac{3}{2}(1+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2})$=$4n+\frac{9}{4}-\frac{3}{2(n+1)}-\frac{3}{2(n+2)}$
点评 该题考查等差数列的通项公式、求和公式,考查裂项求和,属于中档题.


科目:高中数学 来源: 题型:解答题
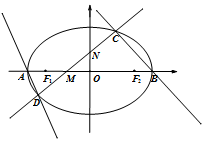 如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,|AB|=4,|F1F2|=2$\sqrt{3}$,直线y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.
如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,|AB|=4,|F1F2|=2$\sqrt{3}$,直线y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄 | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) | [40,45) |
| 受访人数 | 5 | 6 | 15 | 9 | 10 | 5 |
| 支持发展 共享单车人数 | 4 | 5 | 12 | 9 | 7 | 3 |
| 年龄低于35岁 | 年龄不低于35岁 | 合计 | |
| 支持 | |||
| 不支持 | |||
| 合计 |
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
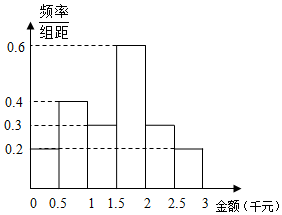 某网络营销部门为了统计某市网友2016年12月12日的网购情况,从该市当天参与网购的顾客中随机抽查了男女各30人,统计其网购金额,得到如下频率分布直方图:
某网络营销部门为了统计某市网友2016年12月12日的网购情况,从该市当天参与网购的顾客中随机抽查了男女各30人,统计其网购金额,得到如下频率分布直方图:| 网购达人 | 非网购达人 | 合计 | |
| 男性 | 30 | ||
| 女性 | 12 | 30 | |
| 合计 | 60 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com