
| 年龄 | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) | [40,45) |
| 受访人数 | 5 | 6 | 15 | 9 | 10 | 5 |
| 支持发展 共享单车人数 | 4 | 5 | 12 | 9 | 7 | 3 |
| 年龄低于35岁 | 年龄不低于35岁 | 合计 | |
| 支持 | |||
| 不支持 | |||
| 合计 |
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)根据表中数据填写2×2列联表,计算K2,对照临界值表即可得出结论;
(2)根据题意知X的可能取值,求出对应的概率值,写出X的分布列,计算数学期望值.
解答 解:(1)根据表中数据填写2×2列联表如下,
| 年龄低于35岁 | 年龄不低于35岁 | 合计 | |
| 支持 | 30 | 10 | 40 |
| 不支持 | 5 | 5 | 10 |
| 合计 | 35 | 15 | 50 |
| X | 2 | 3 | 4 |
| P | $\frac{2}{15}$ | $\frac{7}{15}$ | $\frac{6}{15}$ |
点评 本题考查了独立性检验与离散型随机变量的分布列和数学期望的计算问题,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | $x-\sqrt{2}y=0$ | B. | $\sqrt{2}x-y=0$ | C. | $\sqrt{2}x±y=0$ | D. | $x±\sqrt{2}y=0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{16}$ | B. | $-\frac{2}{5}$ | C. | $\frac{11}{16}$ | D. | $\frac{13}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e2-e+3 | B. | e2+4 | C. | e+1 | D. | e+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
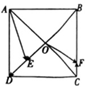 如图,边长为4的正方形ABCD中,AC与BD交于点O,$\overrightarrow{BE}$=$\frac{3}{4}$$\overrightarrow{BD}$,$\overrightarrow{CF}$=$\frac{1}{4}$$\overrightarrow{CB}$,则$\overrightarrow{AE}$•$\overrightarrow{OF}$等于( )
如图,边长为4的正方形ABCD中,AC与BD交于点O,$\overrightarrow{BE}$=$\frac{3}{4}$$\overrightarrow{BD}$,$\overrightarrow{CF}$=$\frac{1}{4}$$\overrightarrow{CB}$,则$\overrightarrow{AE}$•$\overrightarrow{OF}$等于( )| A. | -3 | B. | 3 | C. | -5 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{10}{4}$ | C. | $\frac{{\sqrt{10}}}{2}$ | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com