
| A. | $\frac{7}{16}$ | B. | $-\frac{2}{5}$ | C. | $\frac{11}{16}$ | D. | $\frac{13}{16}$ |
分析 由题意,f(x)在R上周期为2的函数,即f(x+2)=f(x).则f($-\frac{5}{2}$)=f($-\frac{1}{2}$)=$-\frac{1}{2}$+a.
f($\frac{9}{2}$)=f($\frac{1}{2}$)=|$\frac{2}{5}-\frac{1}{2}$|=$\frac{1}{10}$,根据$f(-\frac{5}{2})=f(\frac{9}{2})$,求出a,即可求f(5a)的值.
解答 解:由题意,$f(x)=\left\{\begin{array}{l}x+a,-1≤x<0\\|{\frac{2}{5}-x}|,0≤x<1\end{array}\right.$,
f(x)在R上周期为2的函数,即f(x+2)=f(x).
∴f($-\frac{5}{2}$)=f($-\frac{1}{2}$)=$-\frac{1}{2}$+a.
f($\frac{9}{2}$)=f($\frac{1}{2}$)=|$\frac{2}{5}-\frac{1}{2}$|=$\frac{1}{10}$,
∵$f(-\frac{5}{2})=f(\frac{9}{2})$,即$-\frac{1}{2}$+a=$\frac{1}{10}$,
可得a=$\frac{3}{5}$
则f(5a)=f(3)=f(1)=f(-1)=-1+$\frac{3}{5}$=$-\frac{2}{5}$.
故选B
点评 本题主要考查函数周期的求解,根据条件推导f(x+T)=f(x)的形式是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,$\frac{2}{3}$) | B. | (1,$\frac{3}{2}$) | C. | ($\frac{4}{3}$,$\frac{3}{2}$] | D. | [$\frac{3}{2}$,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
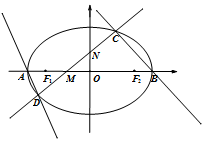 如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,|AB|=4,|F1F2|=2$\sqrt{3}$,直线y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.
如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,|AB|=4,|F1F2|=2$\sqrt{3}$,直线y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | [0,2] | C. | [1,2] | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄 | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) | [40,45) |
| 受访人数 | 5 | 6 | 15 | 9 | 10 | 5 |
| 支持发展 共享单车人数 | 4 | 5 | 12 | 9 | 7 | 3 |
| 年龄低于35岁 | 年龄不低于35岁 | 合计 | |
| 支持 | |||
| 不支持 | |||
| 合计 |
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com