
分析 法一:由已知利用同角三角函数基本关系式可求sin(α+$\frac{π}{3}$),进而利用两角差的余弦函数公式即可计算得解.
法二:由已知利用两角和的余弦函数公式可得sinα=$\frac{\sqrt{3}}{3}$cosα+$\frac{4\sqrt{3}}{9}$,结合同角三角函数基本关系式化简整理可得36cos2α+24cosα-11=0,结合α的范围即可得解.
解答 解:法一:∵α∈(0,$\frac{π}{2}$),cos(α+$\frac{π}{3}$)=-$\frac{2}{3}$,
∴α+$\frac{π}{3}$∈($\frac{π}{3}$,$\frac{5π}{6}$),sin(α+$\frac{π}{3}$)=$\frac{\sqrt{5}}{3}$,
∴cosα=cos[(α+$\frac{π}{3}$)-$\frac{π}{3}$]=cos(α+$\frac{π}{3}$)cos$\frac{π}{3}$+sin(α+$\frac{π}{3}$)sin$\frac{π}{3}$=(-$\frac{2}{3}$)×$\frac{1}{2}$+$\frac{\sqrt{5}}{3}×\frac{\sqrt{3}}{2}$=$\frac{{\sqrt{15}-2}}{6}$.
法二:∵cos(α+$\frac{π}{3}$)=-$\frac{2}{3}$,可得:$\frac{1}{2}$cosα-$\frac{\sqrt{3}}{2}$sinα=-$\frac{2}{3}$,
∴sinα=$\frac{\sqrt{3}}{3}$cosα+$\frac{4\sqrt{3}}{9}$,
又∵sin2α+cos2α=1,
∴($\frac{\sqrt{3}}{3}$cosα+$\frac{4\sqrt{3}}{9}$)2+cos2α=1,整理可得:36cos2α+24cosα-11=0,
∴解得:cosα=$\frac{{\sqrt{15}-2}}{6}$,或$\frac{-2-\sqrt{15}}{6}$.
∵α∈(0,$\frac{π}{2}$),可得:cosα>0,故cosα=$\frac{{\sqrt{15}-2}}{6}$.
故答案为:$\frac{{\sqrt{15}-2}}{6}$.
点评 本题主要考查了两角和的余弦函数公式,同角三角函数基本关系式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{16}$ | B. | $-\frac{2}{5}$ | C. | $\frac{11}{16}$ | D. | $\frac{13}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
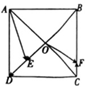 如图,边长为4的正方形ABCD中,AC与BD交于点O,$\overrightarrow{BE}$=$\frac{3}{4}$$\overrightarrow{BD}$,$\overrightarrow{CF}$=$\frac{1}{4}$$\overrightarrow{CB}$,则$\overrightarrow{AE}$•$\overrightarrow{OF}$等于( )
如图,边长为4的正方形ABCD中,AC与BD交于点O,$\overrightarrow{BE}$=$\frac{3}{4}$$\overrightarrow{BD}$,$\overrightarrow{CF}$=$\frac{1}{4}$$\overrightarrow{CB}$,则$\overrightarrow{AE}$•$\overrightarrow{OF}$等于( )| A. | -3 | B. | 3 | C. | -5 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
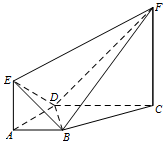 已知几何体ABCDEF中,AB∥CD,AD⊥DC,EA⊥平面ABCD,FC∥EA,AB=AD=EA=1,CD=CF=2.
已知几何体ABCDEF中,AB∥CD,AD⊥DC,EA⊥平面ABCD,FC∥EA,AB=AD=EA=1,CD=CF=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 72.705尺 | B. | 61.395尺 | C. | 61.905尺 | D. | 73.995尺 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{10}{4}$ | C. | $\frac{{\sqrt{10}}}{2}$ | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<-3} | B. | {x|-3<x<2} | C. | {x|x<2} | D. | {x|-3≤x<2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com