
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
分析 可知$|\overrightarrow{a}|=|\overrightarrow{b}|=1$,这样对$|\overrightarrow{a}+3\overrightarrow{b}|=\sqrt{13}$两边平方即可求出$\overrightarrow{a}•\overrightarrow{b}$的值,进而求出cos$<\overrightarrow{a},\overrightarrow{b}>$的值,从而得出$\overrightarrow{a}$与$\overrightarrow{b}$的夹角.
解答 解:$(\overrightarrow{a}+3\overrightarrow{b})^{2}$
=${\overrightarrow{a}}^{2}+6\overrightarrow{a}•\overrightarrow{b}+9{\overrightarrow{b}}^{2}$
=$1+6\overrightarrow{a}•\overrightarrow{b}+9$
=13;
∴$\overrightarrow{a}•\overrightarrow{b}=\frac{1}{2}$;
∴$cos<\overrightarrow{a},\overrightarrow{b}>=\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}=\frac{1}{2}$;
∴$\overrightarrow{a},\overrightarrow{b}$的夹角为$\frac{π}{3}$.
故选C.
点评 考查单位向量的概念,向量数量积的运算,向量夹角的余弦公式,以及向量夹角的范围.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{7}}}{2}$ | B. | $\frac{5}{3}$ | C. | $\frac{{\sqrt{7}}}{3}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
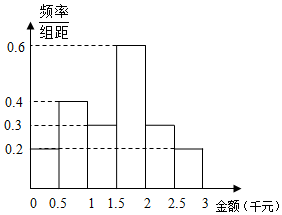 某网络营销部门为了统计某市网友2016年12月12日的网购情况,从该市当天参与网购的顾客中随机抽查了男女各30人,统计其网购金额,得到如下频率分布直方图:
某网络营销部门为了统计某市网友2016年12月12日的网购情况,从该市当天参与网购的顾客中随机抽查了男女各30人,统计其网购金额,得到如下频率分布直方图:| 网购达人 | 非网购达人 | 合计 | |
| 男性 | 30 | ||
| 女性 | 12 | 30 | |
| 合计 | 60 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
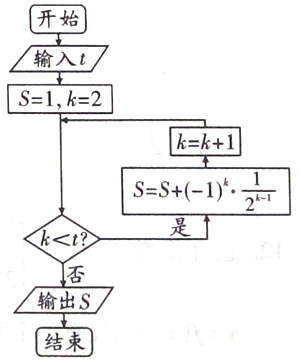
| A. | $\frac{11}{8}$ | B. | $\frac{9}{16}$ | C. | $\frac{5}{4}$ | D. | $\frac{21}{16}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com