
 Ρ≥Άχ¬γ”Σœζ≤ΩΟ≈ΈΣΝΥΆ≥ΦΤΡ≥ –Άχ”―2016Ρξ12‘¬12»’ΒΡΆχΙΚ«ιΩωΘ§¥”ΗΟ –Β±Χλ≤Έ”κΆχΙΚΒΡΙΥΩΆ÷–ΥφΜζ≥ι≤ιΝΥΡ–≈°Ης30»ΥΘ§Ά≥ΦΤΤδΆχΙΚΫπΕνΘ§ΒΟΒΫ»γœ¬ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘΚ
Ρ≥Άχ¬γ”Σœζ≤ΩΟ≈ΈΣΝΥΆ≥ΦΤΡ≥ –Άχ”―2016Ρξ12‘¬12»’ΒΡΆχΙΚ«ιΩωΘ§¥”ΗΟ –Β±Χλ≤Έ”κΆχΙΚΒΡΙΥΩΆ÷–ΥφΜζ≥ι≤ιΝΥΡ–≈°Ης30»ΥΘ§Ά≥ΦΤΤδΆχΙΚΫπΕνΘ§ΒΟΒΫ»γœ¬ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘΚ| ΆχΙΚ¥ο»Υ | Ζ«ΆχΙΚ¥ο»Υ | ΚœΦΤ | |
| Ρ––‘ | 30 | ||
| ≈°–‘ | 12 | 30 | |
| ΚœΦΤ | 60 |
| PΘ®K2ΓίkΘ© | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
Ζ÷Έω Θ®ΔώΘ©άϊ”Ο÷±ΖΫΆΦ÷–ΟΩ“Μ–ΓΉιΒΉΟφ÷–Βψ≥Υ“‘Ε‘”ΠΒΡΤΒ¬ Θ§‘Ό«σΚΆΦΤΥψΤΫΨυ÷ΒΘΜ
Θ®ΔρΘ©ΗυΨίΧβ“βΘ§Χν–¥Ν–ΝΣ±μΘ§ΦΤΥψK2Θ§Ε‘’’ΝΌΫγ÷Β±μΒΟ≥ωΫα¬έΘ°
Ϋβ¥π ΫβΘΚΘ®ΔώΘ©ΦΤΥψΤΫΨυ÷ΒΈΣ
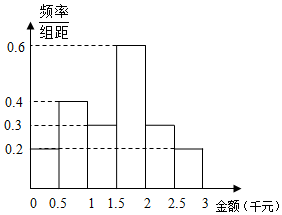
$\overline{x}$=0.25ΓΝ0.1+0.75ΓΝ0.2+1.25ΓΝ0.15+1.75ΓΝ0.3+2.25ΓΝ0.15+2.75ΓΝ0.1
=1.5«ß‘ΣΘΜ Γ≠Θ®6Ζ÷Θ©
Θ®ΔρΘ©ΗυΨίΧβ“βΘ§Χν–¥Ν–ΝΣ±μ»γœ¬ΘΚ
| ΆχΙΚ¥ο»Υ | Ζ«ΆχΙΚ¥ο»Υ | ΚœΦΤ | |
| Ρ––‘ | 3 | 27 | 30 |
| ≈°–‘ | 12 | 18 | 30 |
| ΚœΦΤ | 15 | 45 | 60 |
ΒψΤά ±ΨΧβΩΦ≤ιΝΥΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΒΡ”Π”ΟΈ ΧβΘ§“≤ΩΦ≤ιΝΥΕάΝΔ–‘Φλ―ιΒΡ”Π”ΟΈ ΧβΘ§ «Μυ¥ΓΧβΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | ≥δΖ÷≤Μ±Ί“ΣΧθΦΰ | BΘ° | ±Ί“Σ≤Μ≥δΖ÷ΧθΦΰ | ||
| CΘ° | ≥δ“ΣΧθΦΰ | DΘ° | Φ»≤Μ≥δΖ÷“≤≤Μ±Ί“ΣΧθΦΰ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | $\frac{Π–}{6}$ | BΘ° | $\frac{Π–}{4}$ | CΘ° | $\frac{Π–}{3}$ | DΘ° | $\frac{Π–}{2}$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 72.705≥Ώ | BΘ° | 61.395≥Ώ | CΘ° | 61.905≥Ώ | DΘ° | 73.995≥Ώ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | [-6Θ§4] | BΘ° | [-4Θ§6] | CΘ° | Θ®-4Θ§6Θ© | DΘ° | Θ®-6Θ§4Θ© |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 2 | BΘ° | $\frac{10}{4}$ | CΘ° | $\frac{{\sqrt{10}}}{2}$ | DΘ° | -1 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | {2} | BΘ° | {2Θ§4} | CΘ° | {2Θ§4Θ§6} | DΘ° | ∅ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | $\frac{1}{9}$ | BΘ° | $\frac{1}{3}$ | CΘ° | $\frac{2+\sqrt{3}}{9}$ | DΘ° | $\frac{2-\sqrt{3}}{9}$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com