
| A. | $\frac{1}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{2+\sqrt{3}}{9}$ | D. | $\frac{2-\sqrt{3}}{9}$ |
分析 由三角内角和定理,将原式转化成2sinCcosB=2sin(B+C)+sinB,利用两角和的正弦公式,求得cosC=-$\frac{1}{2}$,再根据余弦定理及基本不等式,求得ab的最小值.
解答 解:在△ABC中,由A+B+C=π知,sinA=sin[π-(B+C)]=sin(B+C),
2sinCcosB=2sinA+sinB,
∴2sinCcosB=2sin(B+C)+sinB,
∴2sinCcosB-2sinBcosC-2cosBsinC=sinB,
∴-2sinBcosC=sinB,
由sinB>0,
∴cosC=-$\frac{1}{2}$,
∵c=3ab,
∴由余弦定理可得c2=a2+b2-2ab•cosC,
整理可得9a2b2=a2+b2+ab≥3ab,当且仅当a=b取等号,
∴ab≥$\frac{1}{3}$,则ab的最小值是$\frac{1}{3}$.
故选:B.
点评 本题主要考查正弦定理和余弦定理的应用,诱导公式、两角和的正弦公式、基本不等式的应用,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
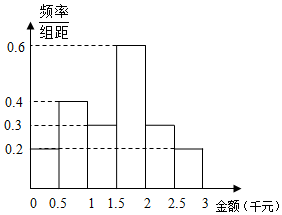 某网络营销部门为了统计某市网友2016年12月12日的网购情况,从该市当天参与网购的顾客中随机抽查了男女各30人,统计其网购金额,得到如下频率分布直方图:
某网络营销部门为了统计某市网友2016年12月12日的网购情况,从该市当天参与网购的顾客中随机抽查了男女各30人,统计其网购金额,得到如下频率分布直方图:| 网购达人 | 非网购达人 | 合计 | |
| 男性 | 30 | ||
| 女性 | 12 | 30 | |
| 合计 | 60 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 12 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,3) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>1)的左焦点F与抛物线y2=-4x的焦点重合,直线x-y+$\frac{\sqrt{2}}{2}$=0与以原点O为圆心,以椭圆的离心率e为半径的圆相切.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>1)的左焦点F与抛物线y2=-4x的焦点重合,直线x-y+$\frac{\sqrt{2}}{2}$=0与以原点O为圆心,以椭圆的离心率e为半径的圆相切.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
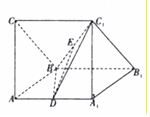 在如图所示的直三棱柱ABC-A1B1C1中,面AA1B1B和面AA1C1C都是边长为1的正方形且互相垂直,D为AA1的中点,E为BC1的中点.
在如图所示的直三棱柱ABC-A1B1C1中,面AA1B1B和面AA1C1C都是边长为1的正方形且互相垂直,D为AA1的中点,E为BC1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com