
 ��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��1������F��������y2=-4x�Ľ����غϣ�ֱ��x-y+$\frac{\sqrt{2}}{2}$=0����ԭ��OΪԲ�ģ�����Բ��������eΪ�뾶��Բ���У�
��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��1������F��������y2=-4x�Ľ����غϣ�ֱ��x-y+$\frac{\sqrt{2}}{2}$=0����ԭ��OΪԲ�ģ�����Բ��������eΪ�뾶��Բ���У����� �⣺��1��ͨ�������߷��̿�֪c=1�����õ㵽ֱ�ߵľ��빫ʽ��֪e=$\frac{|0-0+\frac{\sqrt{2}}{2}|}{\sqrt{2}}$=$\frac{1}{2}$�����a��b��c����֮��Ĺ�ϵ�����a=2��b=1�������ɵ���ԲC�ķ��̣�
��2��ͨ���������ֱ��ABʹ��S1=S2��������䷽��Ϊ��y=k��x+1����k��0����������ԲC�������������Τ�ﶨ���ɵ�G��$\frac{-4{k}^{2}}{4{k}^{2}+3}$��$\frac{3k}{4{k}^{2}+3}$��������DG��AB�ɵ�D��$\frac{-{k}^{2}}{4{k}^{2}+3}$��0������ϡ�GFD����OED�ɵ�$\frac{{S}_{1}}{{S}_{2}}$=$��{\frac{|DG|}{|OD|}��}^{2}$������S1=S2������8k2+9=0�����ڴ˷������Ƴ����費������
��� �⣺��1�������⣬֪��c=1��e=$\frac{|0-0+\frac{\sqrt{2}}{2}|}{\sqrt{2}}$=$\frac{1}{2}$��$\frac{c}{a}$=$\frac{1}{2}$��
��a=2��b=1��
�����ԲC�ķ���Ϊ��$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1��
��2�����ۣ�������ֱ��AB��ʹ��S1=S2��
�������£�
�������ֱ��AB��ʹ��S1=S2����Ȼֱ��AB������x��y�ᴹֱ��
����ֱ��AB��б�ʴ��ڣ����䷽��Ϊ��y=k��x+1����k��0����
����ֱ��AB����ԲC���̣���ȥy�ã���4k2+3��x2+8k2x+4k2-12=0��
��A��x1��y2����B��x2��y2������
x1+x2=$\frac{-8{k}^{2}}{4{k}^{2}+3}$��y1+y2=k��x1+x2��+2=$\frac{6k}{4{k}^{2}+3}$��
����G��$\frac{-4{k}^{2}}{4{k}^{2}+3}$��$\frac{3k}{4{k}^{2}+3}$����
��DG��AB���ã�$\frac{{y}_{G}}{{x}_{G}-{x}_{D}}$��k=-1����ã�xD=$\frac{-{k}^{2}}{4{k}^{2}+3}$����D��$\frac{-{k}^{2}}{4{k}^{2}+3}$��0����
��Ϊ��GFD����OED������$\frac{|GF|}{|OE|}$=$\frac{|DG|}{|OD|}$������$\frac{|GF|}{|OE|}$•$\frac{|DG|}{|OD|}$=$��{\frac{|DG|}{|OD|}��}^{2}$����$\frac{{S}_{1}}{{S}_{2}}$=$��{\frac{|DG|}{|OD|}��}^{2}$��
����ΪS1=S2������|GD|=|OD|��
����$\sqrt{��\frac{-{k}^{2}}{4{k}^{2}+3}-\frac{-4{k}^{2}}{4{k}^{2}+3}��^{2}+��\frac{3k}{4{k}^{2}+3}��^{2}}$=|$\frac{-{k}^{2}}{4{k}^{2}+3}$|��
�����ã�8k2+9=0�����ڴ˷����⣬�ʲ�����ֱ��AB��ʹ��S1=S2��
���� ������һ��ֱ����Բ���ߵ��ۺ��⣬���������������������ת���뻯��˼�롢����˼�룬������Բ���̡�ֱ�߷��̡����������εȻ���֪ʶ��ע����ⷽ���Ļ��ۣ������е��⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {2} | B�� | {2��4} | C�� | {2��4��6} | D�� | ∅ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{9}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{2+\sqrt{3}}{9}$ | D�� | $\frac{2-\sqrt{3}}{9}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
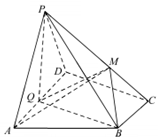 ��ͼ��������P-ABCD�У�����ABCDΪֱ�����Σ�AD��BC����ADC=90�㣬ƽ��PAD�A����ABCD��QΪAD���е㣬M����PC�ϵĵ㣬PA=PD��BC=$\frac{1}{2}$AD
��ͼ��������P-ABCD�У�����ABCDΪֱ�����Σ�AD��BC����ADC=90�㣬ƽ��PAD�A����ABCD��QΪAD���е㣬M����PC�ϵĵ㣬PA=PD��BC=$\frac{1}{2}$AD�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
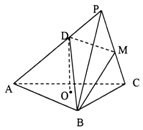 ��ͼ������P-ABC�У�����ABCΪ�ȱ������Σ�OΪ��ABC�����ģ�ƽ��PBC��ƽ��ABC��PB=PC=BC=$\sqrt{3}$��DΪAP��һ�㣬��AD=2DP��
��ͼ������P-ABC�У�����ABCΪ�ȱ������Σ�OΪ��ABC�����ģ�ƽ��PBC��ƽ��ABC��PB=PC=BC=$\sqrt{3}$��DΪAP��һ�㣬��AD=2DP���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com