
分析 (Ⅰ)f′(x)=ex+2x-1,f′(0)=0,由导数性质得f(x)是(0,+∞)上的增函数,是(-∞,0)上的减函数,由此能求出f(x)的零点个数.
(Ⅱ)当x∈[-1,1]时,f(x)max-f(x)min≥e-1,f′(x)=axlna+2x-lna=2x+(ax-1)lna,由导数性质得f(x)是[-1,0]上的减函数,[0,1]上的增函数,由此利用导数性质和构造法能求出a的取值范围.
解答 解:(Ⅰ)f(x)=ex+x2-x-4,
∴f′(x)=ex+2x-1,∴f′(0)=0,
当x>0时,ex>1,∴f′(x)>0,故f(x)是(0,+∞)上的增函数,
当x<0时,ex<1,∴f′(x)<0,
故f(x)是(-∞,0)上的减函数,…(3分)
f(1)=e-4<0,f(2)=e2-2>0,
∴存在x1∈(1,2)是f(x)在(0,+∞)上的唯一零点,
$f(-2)=\frac{1}{{e}^{2}}+2>0,f(-1)=\frac{1}{e}-2<0$,
∴存在x2∈(-2,-1)是f(x)在(-∞,0)上的唯一零点,
∴f(x)的零点个数为2…(6分)
(Ⅱ)当x∈[-1,1]时,f(x)max-f(x)min≥e-1,
f′(x)=axlna+2x-lna=2x+(ax-1)lna,
当x>0时,由a>1,可知ax-1>0,lna>0,∴f′(x)>0;
当x<0时,由a>1,可知ax-1<0,lna>0,
∴f'(x)<0;当x=0时,f′(x)=0,
∴f(x)是[-1,0]上的减函数,[0,1]上的增函数..…(8分)
∴当x∈[-1,1]时,f(x)min=f(0),f(x)max为f(-1)和f(1)中的较大者.$而f(1)-f(-1)=a-\frac{1}{a}-2lna,设g(x)=x-\frac{1}{x}-2lnx(x>0)$,∵${g}^{'}(x)=1+\frac{1}{{x}^{2}}-\frac{2}{x}={(\frac{1}{x}-1)}^{2}≥0(当且仅当x=1时等号成立)$,
∴g(x)在(0,+∞)上单调递增,而g(1)=0,
∴$当t>1时,g(x)>0即a>1时,a-\frac{1}{a}-2lna≥0$,
∴f(1)>f(-1).…(10分)
∴f(1)-f(0)≥e-1,即a-lna≥e-1=e-lne,
设h(a)=a-lna(a>1),∴h′(a)>0,
∴h(a)在(1,+∞)递增,∴a≥e,即a的取值范围是[e,+∞).…(12分)
点评 本题考查函数的零点个数的求法,考查实数的取值范围的求法,考查导数的性质及应用等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、分类与整合思想,是中档题.


科目:高中数学 来源: 题型:解答题
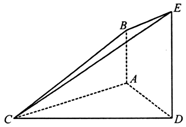 如图,已知AB⊥平面ACD,DE∥AB,△ACD是等腰三角形,∠CAD=120°,AD=DE=2AB.
如图,已知AB⊥平面ACD,DE∥AB,△ACD是等腰三角形,∠CAD=120°,AD=DE=2AB.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{5}$,+∞) | B. | [$\frac{1}{5}$,+∞) | C. | (1,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | ($\sqrt{2}$,+∞) | C. | (2,+∞) | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
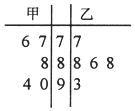
| A. | 甲乙得分的中位数相同 | B. | 乙的成绩较甲更稳定 | ||
| C. | 甲的平均分比乙高 | D. | 乙的平均分低于其中位数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $x-\sqrt{2}y=0$ | B. | $\sqrt{2}x-y=0$ | C. | $\sqrt{2}x±y=0$ | D. | $x±\sqrt{2}y=0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{16}$ | B. | $-\frac{2}{5}$ | C. | $\frac{11}{16}$ | D. | $\frac{13}{16}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com