练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．如图茎叶图表示一次朗诵比赛中甲乙两位选手的得分，则下列说法错误的是（　　）
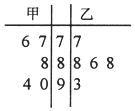
    A．甲乙得分的中位数相同B．乙的成绩较甲更稳定
    C．甲的平均分比乙高D．乙的平均分低于其中位数

    分析 根据茎叶图中的数据，对选项中的命题进行分析、判断正误即可．

    解答 解：根据茎叶图中的数据知，
    甲的中位数为88，乙的中位数为88，二者相同，A正确；
    甲的数据集中在76～94之间，不成单峰分布，
    乙的数据集中在77～93之间，成单峰分布，
    ∴乙的成绩更稳定，B正确；
    甲的平均数是$\overline{{x}_{甲}}$=$\frac{1}{5}$×（76+77+88+90+94）=85，
    乙的平均数是$\overline{{x}_{乙}}$=$\frac{1}{5}$×（77+88+86+88+93）=86.4，
    甲的平均数比乙的低，∴C错误；
    乙的中位数是88，平均数是86.4，平均数比中位数低，D正确．
    故选：C．

    点评 本题考查了根据茎叶图中的数据求中位数、方差、平均数的应用问题，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    16．已知复数z1=$\frac{m-i}{i}$（m∈R）与z2=2i的虚部相等，则复数z1对应的点在（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．在△ABC中，角A、B、C对边分别为a、b、c，a2+b2+c2=ab+bc+ca．
    （1）证明△ABC是正三角形；
    （2）如图，点D在边BC的延长线上，且BC=2CD，AD=$\sqrt{7}$，求sin∠BAD的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．己知函数f（x）=a2+x2-xlna-b（a，b∈R，a＞1），e自然对数的底数．
    （Ⅰ）当a=e，b=4时，求函数f（x）零点个数
    （Ⅱ）若b=1，求f（x）在[-1，1]上的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

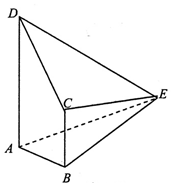    1．如图，在四棱锥E-ABCD中，平面CDE⊥平面ABCD，∠DAB=∠ABC=90°，AB=BC=1，AD=ED=3，EC=2．
    （1）证明：AB⊥平面BCE；
    （2）求直线AE与平面CDE所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．函数y=$\frac{1}{{\sqrt{{{log}_2}（{3x-2}）}}}$的定义域为{x|x＞1}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．某学校共3000名学生，其中高一年级900人，现用分层抽样的方式从三个年级中抽取部分学生进行心理测试，已知高一年级抽取了6人，则样本容量为20．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知x∈R，符号[x]表示不超过x的最大整数，f（x）=$\left\{\begin{array}{l}{[x]，x≤0}\\{\frac{1}{x}，x＞0}\end{array}\right.$，则使方程$\frac{f（x）}{x}$=m恰有三个实根的实数m的取值范围是（　　）
    A．（$\frac{1}{2}$，$\frac{2}{3}$）B．（1，$\frac{3}{2}$）C．（$\frac{4}{3}$，$\frac{3}{2}$]D．[$\frac{3}{2}$，2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．若函数f（x）=$\left\{\begin{array}{l}{x^3}+e，x≤0\\ \frac{e^x}{x}，x＞0\end{array}$，则方程f（f（x））=$\frac{e^3}{3}$的根的个数为（　　）
    A．4B．3C．2D．1

    查看答案和解析>>

    同步练习册答案