
分析 根据题意逐一得到A1A5=$\frac{1}{32}$,PA1=QA1=$\frac{1}{2}$,问题得以解决
解答 解:由题意可得PA1=QA1=$\frac{1}{2}$,
A1A2=$\frac{1}{2}$QA1=$\frac{1}{4}$,
A2A3=A1A3=$\frac{1}{2}$A1A2=$\frac{1}{8}$,
A3A4=$\frac{1}{2}$A2A3=$\frac{1}{16}$,
A4A5=A3A5=$\frac{1}{2}$A3A4=$\frac{1}{32}$,
∴PA5=PA1+A1A3+A3A5=$\frac{1}{2}$+$\frac{1}{8}$+$\frac{1}{32}$=$\frac{21}{32}$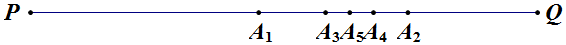
故答案为:$\frac{21}{32}$
点评 本题考查了归纳推理的问题,关键找到规律,属于基础题


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | [0,2] | C. | [1,2] | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 方程f(x)=0有两个不相等的整数根 | B. | 方程f(x)=0没有整数根 | ||
| C. | 方程f(x)=0至少有一个整数根 | D. | 方程f(x)=0至多有一个整数根 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄 | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) | [40,45) |
| 受访人数 | 5 | 6 | 15 | 9 | 10 | 5 |
| 支持发展 共享单车人数 | 4 | 5 | 12 | 9 | 7 | 3 |
| 年龄低于35岁 | 年龄不低于35岁 | 合计 | |
| 支持 | |||
| 不支持 | |||
| 合计 |
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
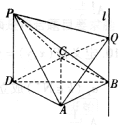 四棱锥P-ABCD中,PD⊥面ABCD,底面ABCD是菱形,且PD=DA=2,∠CDA=60°,过点B作直线l∥PD,Q为直线l上一动点.
四棱锥P-ABCD中,PD⊥面ABCD,底面ABCD是菱形,且PD=DA=2,∠CDA=60°,过点B作直线l∥PD,Q为直线l上一动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | (0,0) | C. | (4,6) | D. | (2,6) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com