
| A. | 方程f(x)=0有两个不相等的整数根 | B. | 方程f(x)=0没有整数根 | ||
| C. | 方程f(x)=0至少有一个整数根 | D. | 方程f(x)=0至多有一个整数根 |
分析 先通过条件得到a,b同奇偶,然后分别讨论若a,b同为偶数与同为奇数两种情形,然后根据数值的奇偶进行判定方程有无整数根.
解答 证明:f(0)=c为奇数,
f(1)=a+b+c为奇数,则a+b为偶数,
所以a,b同奇偶,
假设整数根t,所以f(t)=0 即at2+bt+c=0,
若a,b同为偶数,则at2+bt为偶数,
所以at2+bt+c为奇数可得at2+bt+c≠0
与at2+bt+c=0矛盾;
若a,b同为奇数,若t为偶数则at2+bt为偶数,
若t为奇数则at2+bt为偶数,
所以 at2+bt+c为奇数 可得at2+bt+c≠0与at2+bt+c=0矛盾.
综上所述方程f(x)=0无整数根;
故选:B
点评 本题主要考查了函数与方程的综合运用,以及分类讨论的数学思想,属于中档题.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 参加跳绳的同学 | 未参加跳绳的同学 | |
| 参加踢毽的同学 | 9 | 4 |
| 未参加踢毽的同学 | 7 | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $4\sqrt{3}+3\sqrt{7}$ | B. | $4\sqrt{7}+3\sqrt{3}$ | C. | ${(4\sqrt{3}+3\sqrt{7})^2}$ | D. | ${(4\sqrt{7}+3\sqrt{3})^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
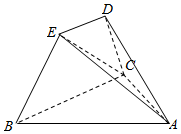 如图所示,四棱锥A-BCDE,已知平面BCDE⊥平面ABC,BE⊥EC,DE∥BC,BC=2DE=6,AB=4$\sqrt{3}$,∠ABC=30°.
如图所示,四棱锥A-BCDE,已知平面BCDE⊥平面ABC,BE⊥EC,DE∥BC,BC=2DE=6,AB=4$\sqrt{3}$,∠ABC=30°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com