
| �μ�������ͬѧ | δ�μ�������ͬѧ | |
| �μ���릵�ͬѧ | 9 | 4 |
| δ�μ���릵�ͬѧ | 7 | 20 |
���� ��1���ɱ���֪���Ȳμ������ֲμ���릵�ͬѧ9�ˣ�ֻ�μ���릵�ͬѧ4�ˣ�ֻ�μ�������ͬѧ7�ˣ��ɴ��������ͬѧ���ٲμ�����һ���ĸ��ʣ�
��2����5����ͬѧΪ�ף�1��2��3��4��4��ŮͬѧΪ�ң�5��6��7���ɴ������оٷ����������5��������4��Ů���и������ѡ1�ˣ���ͬѧ��δ��ѡ����Ůͬѧ�ұ�ѡ�еĸ��ʣ�
��� �⣺��1���ɱ���֪���Ȳμ������ֲμ���릵�ͬѧ9�ˣ�ֻ�μ���릵�ͬѧ4�ˣ�
ֻ�μ�������ͬѧ7�ˣ��������ٲμ�����һ����ͬѧ��20�ˣ�
�衰��ͬѧ���ٲμ�����һ����Ϊ�¼�A����$P��A��=\frac{20}{40}=\frac{1}{2}$��
��2����5����ͬѧΪ�ף�1��2��3��4��4��ŮͬѧΪ�ң�5��6��7��
���п��ܵĽ���У����ף��ң������ף�5�������ף�6�������ף�7����
��1���ң�����1��5������1��6������1��7������2���ң�����2��5����
��2��6������2��7������3���ң�����3��5������3��6������3��7����
��4���ң�����4��5������4��6������4��7��������20�֣�
�ǡ���ͬѧ��δ��ѡ����Ůͬѧ�ұ�ѡ�С�Ϊ�¼�B��
��B��������1���ң�����2���ң�����3���ң�����4���ң�����4�������
����ͬѧ��δ��ѡ����Ůͬѧ�ұ�ѡ�еĸ���$P��B��=\frac{4}{20}=\frac{1}{5}$��
���� ���⿼����ʵ����ǻ����⣬����ʱҪ�������⣬ע���оٷ��ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{3}$ | B�� | $-\frac{1}{3}$ | C�� | $-\frac{3}{7}$ | D�� | $\frac{3}{7}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ?x0��R��ʹ��x02-x0+2=0 | |
| B�� | ���⡰?x��R��x2+x+1��0���ķ��ǡ�?x0��R��x02+x0+1��0�� | |
| C�� | ?�ȡ�R������f��x��=sin��2x+�ȣ�������ż���� | |
| D�� | �ڡ�ABC�У���A=B���ǡ�sinA=sinB���ij�Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����f��x��=0����������ȵ������� | B�� | ����f��x��=0û�������� | ||
| C�� | ����f��x��=0������һ�������� | D�� | ����f��x��=0������һ�������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-$\frac{��}{3}$��$\frac{��}{6}$] | B�� | [-$\frac{��}{3}$��$\frac{2��}{3}$] | C�� | [-$\frac{��}{6}$��$\frac{5��}{6}$] | D�� | [$\frac{��}{6}$��$\frac{2��}{3}$] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
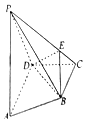 ��ͼ������P-ABCD�У�AD��BC��AD��DC��AD=2BC=2���ڲ���PAD�У�PA=PD��EΪ����PC�ϲ�ͬ�ڶ˵������һ����PA��DE��
��ͼ������P-ABCD�У�AD��BC��AD��DC��AD=2BC=2���ڲ���PAD�У�PA=PD��EΪ����PC�ϲ�ͬ�ڶ˵������һ����PA��DE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com