
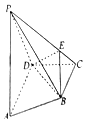
 如图,四棱锥P-ABCD中,AD∥BC,AD⊥DC,AD=2BC=2,在侧面PAD中,PA=PD,E为侧棱PC上不同于端点的任意一点且PA⊥DE.
如图,四棱锥P-ABCD中,AD∥BC,AD⊥DC,AD=2BC=2,在侧面PAD中,PA=PD,E为侧棱PC上不同于端点的任意一点且PA⊥DE.分析 (1)推导出PA⊥平面PCD,从而PA⊥CD,再由AD⊥DC,推导出CD⊥平面PAD,由此能证明平面PAD⊥平面ABCD.
(2)连结AC,交BD于O,连结OE,推导出PA∥OE,从而$\frac{CE}{PE}=\frac{CO}{AO}$,由此能求出结果.
解答 证明:(1)∵E是侧棱PC上不同于端点的任意一点,且PA⊥DE,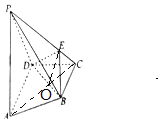
∴PA⊥平面PCD,
∵CD?平面PCD,∴PA⊥CD,
∵AD⊥DC,PA∩AD=A,PA,AD?平面PAD,
∴CD⊥平面PAD,
∵CD?平面ABCD,∴平面PAD⊥平面ABCD.
解:(2)连结AC,交BD于O,连结OE,
∴平面PAD∩平面BDE于O,
∵PA∥平面BDE,PA?平面PAC,
∴PA∥OE,∴$\frac{CE}{PE}=\frac{CO}{AO}$,
∵AD∥BC,AD=2BC,
∴$\frac{CO}{AO}=\frac{CB}{AD}=\frac{1}{2}$,
∴$\frac{CE}{PE}$=$\frac{1}{2}$.
点评 本题考查面面垂直的证明,考查两线段比值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、数形结合思想,是中档题.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | f(1)<2016f($\root{3}{2016}$)<2017f($\root{3}{2017}$) | B. | 2017f($\root{3}{2017}$)<f(1)<2016f($\root{3}{2016}$) | ||
| C. | 2016f($\root{3}{2016}$)<f(1)<2017f($\root{3}{2017}$) | D. | 2017f($\root{3}{2017}$)<2016f($\root{3}{2016}$)<f(1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 参加跳绳的同学 | 未参加跳绳的同学 | |
| 参加踢毽的同学 | 9 | 4 |
| 未参加踢毽的同学 | 7 | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $4\sqrt{3}+3\sqrt{7}$ | B. | $4\sqrt{7}+3\sqrt{3}$ | C. | ${(4\sqrt{3}+3\sqrt{7})^2}$ | D. | ${(4\sqrt{7}+3\sqrt{3})^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
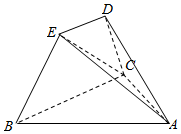 如图所示,四棱锥A-BCDE,已知平面BCDE⊥平面ABC,BE⊥EC,DE∥BC,BC=2DE=6,AB=4$\sqrt{3}$,∠ABC=30°.
如图所示,四棱锥A-BCDE,已知平面BCDE⊥平面ABC,BE⊥EC,DE∥BC,BC=2DE=6,AB=4$\sqrt{3}$,∠ABC=30°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -10 | B. | -5 | C. | 0 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com