
| A. | $4\sqrt{3}+3\sqrt{7}$ | B. | $4\sqrt{7}+3\sqrt{3}$ | C. | ${(4\sqrt{3}+3\sqrt{7})^2}$ | D. | ${(4\sqrt{7}+3\sqrt{3})^2}$ |
分析 设$\overrightarrow{OA}=\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则由向量的数量积运算公式可知${(\overrightarrow a-\overrightarrow b)^2}{(\overrightarrow a-\overrightarrow c)^2}-{[(\overrightarrow a-\overrightarrow b)•(\overrightarrow a-\overrightarrow c)]^2}$最大值为4S${\;}_{△ABC}^{2}$,根据A点轨迹找出A到BC的最大距离即可求出最大值.
解答 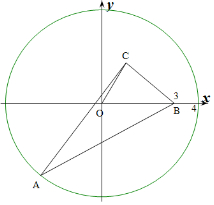 解:设$\overrightarrow{OA}=\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,$\overrightarrow{a}-\overrightarrow{b}$与$\overrightarrow{a}-\overrightarrow{c}$所成夹角为θ,
解:设$\overrightarrow{OA}=\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,$\overrightarrow{a}-\overrightarrow{b}$与$\overrightarrow{a}-\overrightarrow{c}$所成夹角为θ,
则${(\overrightarrow a-\overrightarrow b)^2}{(\overrightarrow a-\overrightarrow c)^2}-{[(\overrightarrow a-\overrightarrow b)•(\overrightarrow a-\overrightarrow c)]^2}$=|AB|2|AC|2-|AB|2|AC|2cos2θ=|AB|2|AC|2sin2θ=|AB|2|AC|2sin2∠CAB,
=4S2△ABC,
∵$|{\overrightarrow b}|=3$,$|{\overrightarrow c}|=2$,$\overrightarrow b•\overrightarrow c=3$,∴$\overrightarrow{b},\overrightarrow{c}$的夹角为60°,
设B(3,0,),C(1,$\sqrt{3}$),则|BC|=$\sqrt{7}$,
∴S△OBC=$\frac{1}{2}×3×2×sin60°$=$\frac{3\sqrt{3}}{2}$,设O到BC的距离为h,
则$\frac{1}{2}•BC•h$=S△OBC=$\frac{3\sqrt{3}}{2}$,
∴h=$\frac{3\sqrt{21}}{7}$,
∵|$\overrightarrow{a}$|=4,∴A点落在以O为圆心,以4为半径的圆上,
∴A到BC的距离最大值为4+h=4+$\frac{3\sqrt{21}}{7}$.
∴S△ABC的最大值为$\frac{1}{2}$×$\sqrt{7}$×(4+$\frac{3\sqrt{21}}{7}$)=2$\sqrt{7}$+$\frac{3\sqrt{3}}{2}$,
∴${(\overrightarrow a-\overrightarrow b)^2}{(\overrightarrow a-\overrightarrow c)^2}-{[(\overrightarrow a-\overrightarrow b)•(\overrightarrow a-\overrightarrow c)]^2}$最大值为4(2$\sqrt{7}$+$\frac{3\sqrt{3}}{2}$)2=(4$\sqrt{7}$+3$\sqrt{3}$)2.
故选:D.
点评 本题考查了平面向量的数量积运算,平面向量在几何中的应用,属于中档题.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 方程f(x)=0有两个不相等的整数根 | B. | 方程f(x)=0没有整数根 | ||
| C. | 方程f(x)=0至少有一个整数根 | D. | 方程f(x)=0至多有一个整数根 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{π}{3}$,$\frac{π}{6}$] | B. | [-$\frac{π}{3}$,$\frac{2π}{3}$] | C. | [-$\frac{π}{6}$,$\frac{5π}{6}$] | D. | [$\frac{π}{6}$,$\frac{2π}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
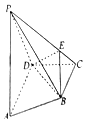 如图,四棱锥P-ABCD中,AD∥BC,AD⊥DC,AD=2BC=2,在侧面PAD中,PA=PD,E为侧棱PC上不同于端点的任意一点且PA⊥DE.
如图,四棱锥P-ABCD中,AD∥BC,AD⊥DC,AD=2BC=2,在侧面PAD中,PA=PD,E为侧棱PC上不同于端点的任意一点且PA⊥DE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{2}$ | B. | $\frac{15}{2}$ | C. | $\frac{21}{2}$ | D. | $\frac{49}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{2}}}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{6}}}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com